- 본 게시글은 Justin Johnson 교수님의 Deep Learning for Computer Vision, University of Michigan 정리글입니다.
- 개인적인 생각이 서술되어 있습니다. 잘못된 내용이 존재할 확률이 존재하기에 주의 바랍니다.
- 잘못된 내용, 오타는 지적해 주시면 감사하겠습니다.
강의링크:
https://www.youtube.com/watch?v=ANyxBVxmdZ0&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=7
강의자료:
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture07.pdf
기타 자료: 고려대학교 김성범 교수님(DMQA) 강의자료 및 강의영상
https://www.youtube.com/watch?v=4AuCBqPvmcc
A brief introduction to CNN
오늘은 딥러닝의 꽃, CNN에 관한 공부를 진행해 보겠습니다. 7강에서는 CNN의 구조를 자세히 알아봅니다.
Convolutional Network의 구성요소는 Fully-Connected Layers, Activation Function, Convolution Layers, Pooling Layers, Normalization입니다.

근데 왜 CNN이 딥러닝의 한 획을 그었다고 평가될까요?

이미지의 경우 각각의 픽셀을 하나의 변수로 간주합니다.
이는 400 X 700 size 이미지 학습을 위해 400 x 700 x 3(R,G,B color) = 840,000는 엄청난 input 파라미터가 생성됨을 의미 → 엄청난 가중치가 생성됨을 의미 → 학습이 매우 어려움을 뜻합니다.
학습을 쉽게 하려면, 파라미터 수를 먼저 줄여야 합니다.

이미지의 특성을 알아야 파라미터 수를 줄일 수 있습니다. spatially-local correlation, invariant feature은 이미지의 특성입니다. 그리고 이를 고려 & 실현한 방법이 바로, Convolution입니다.
- spatially-local correlation: 이미지는 인접 변수간 높은 상관관계를 가짐 → 인접한 변수만으로 새로운 feature 생성
- invariant feature: 이미지의 부분적 특성은 고정된 위치에 등장 X → 인접한 변수 집합에는 동일한 weight를 적용
Convolution Layer

Input으로 3X32X32 size의 이미지가 입력된다고 해보겠습니다. 3은 depth /channel이라 불리며, 맨 처음 input에서의 3은 R,G,B color로 볼 수 있습니다. 32, 32는 width, height를 의미합니다. filter의 size는 3X5X5입니다.
*맨 처음 input을 강조한 이유는, 맨 처음 input 이후의 layer부터, # of channel = # of filter이기 때문입니다.
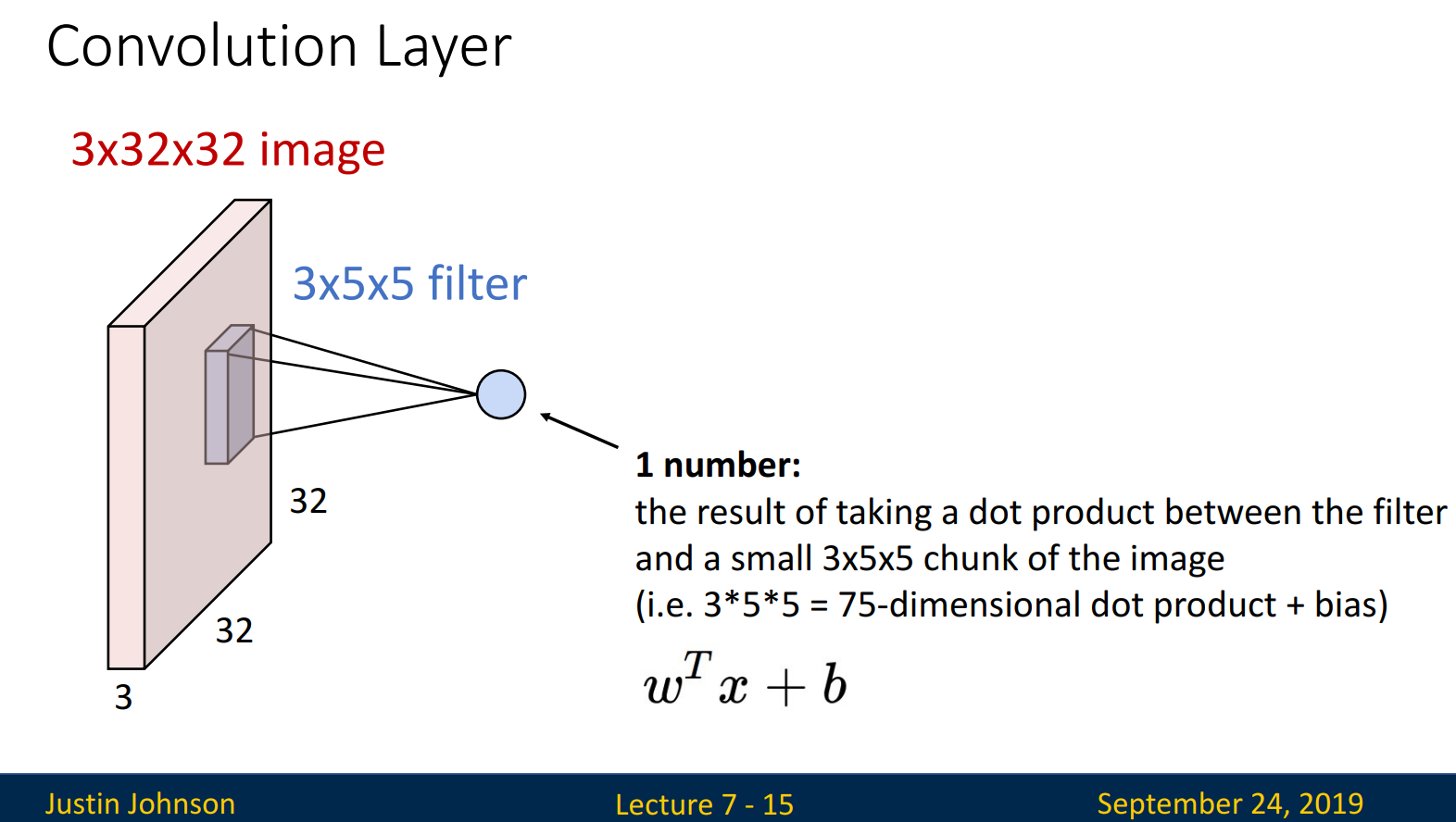
input 이미지와 filter가 합성곱 연산을 수행합니다. Weight matrix와 연산을 수행한 후, bias를 더해줍니다. Filter는 이미지를 순차적으로 지나가며 합성곱 연산을 수행합니다.
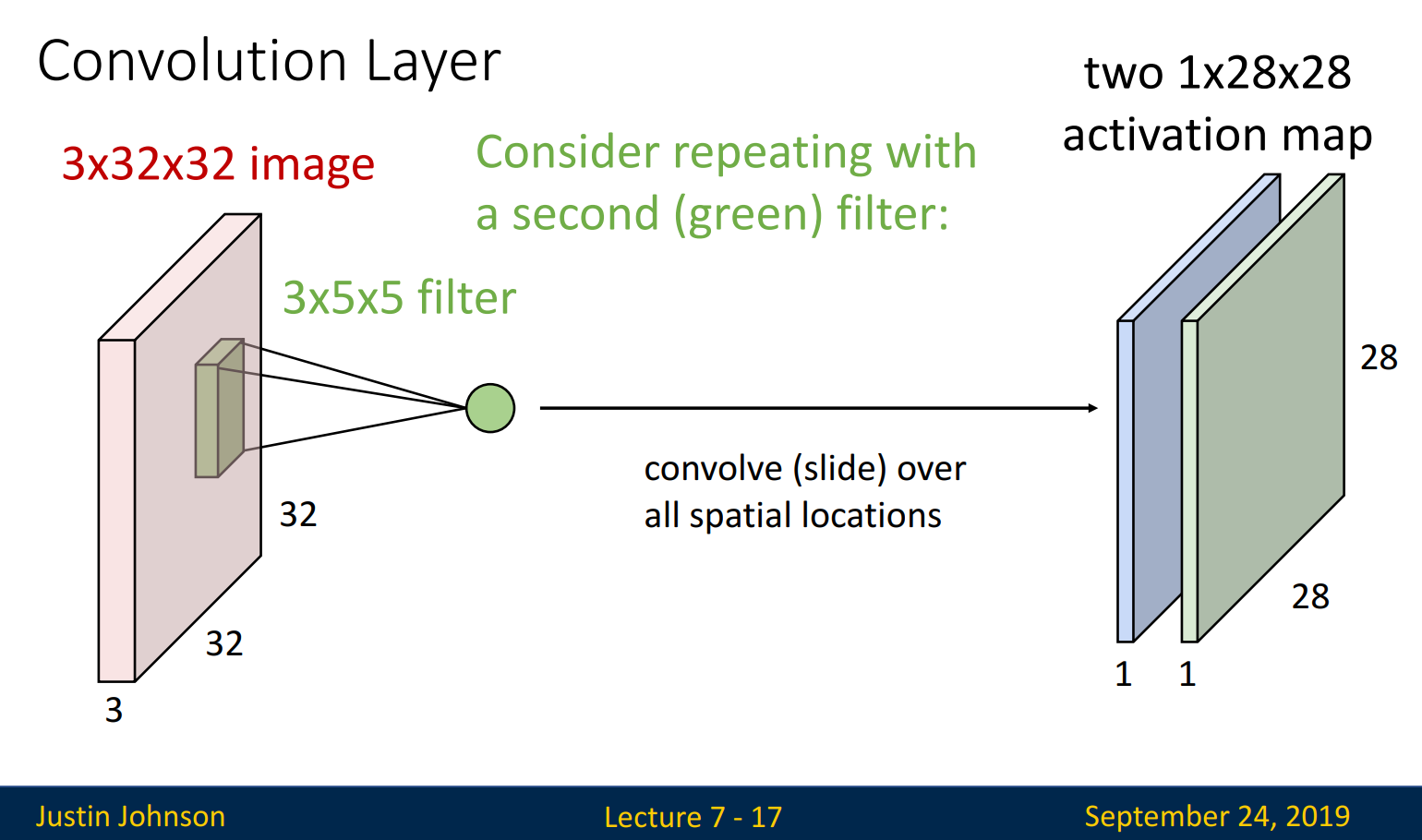
Filtering이 끝난 후 나온 layer를 activation map(=feature map)이라 부립니다. Activation map의 size는 1x28x28로, 조금 있다가 배우게 될 계산식을 통해 계산할 수 있습니다.
* # of filter = # of activation map입니다.
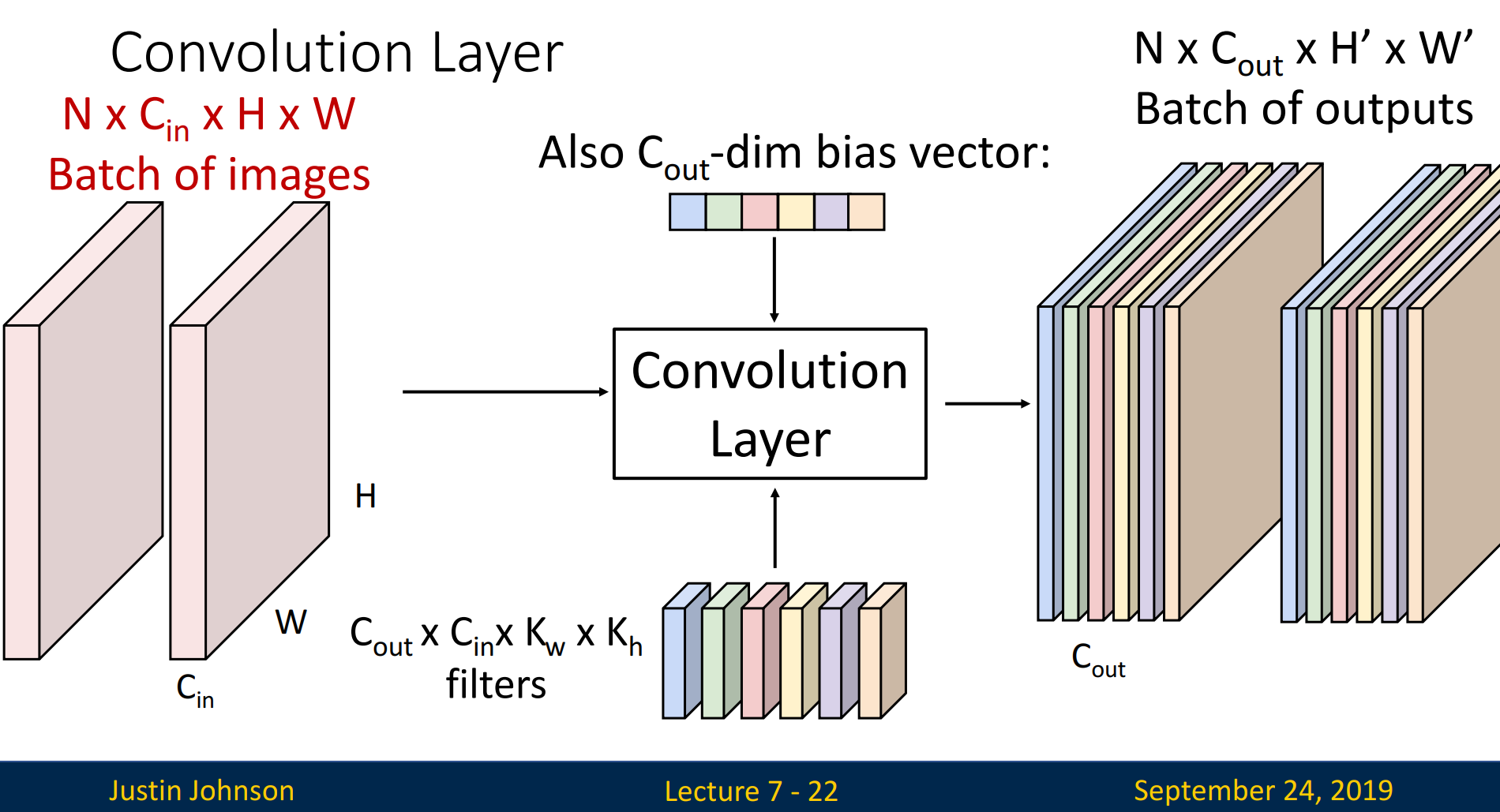
Stacking Convolutions
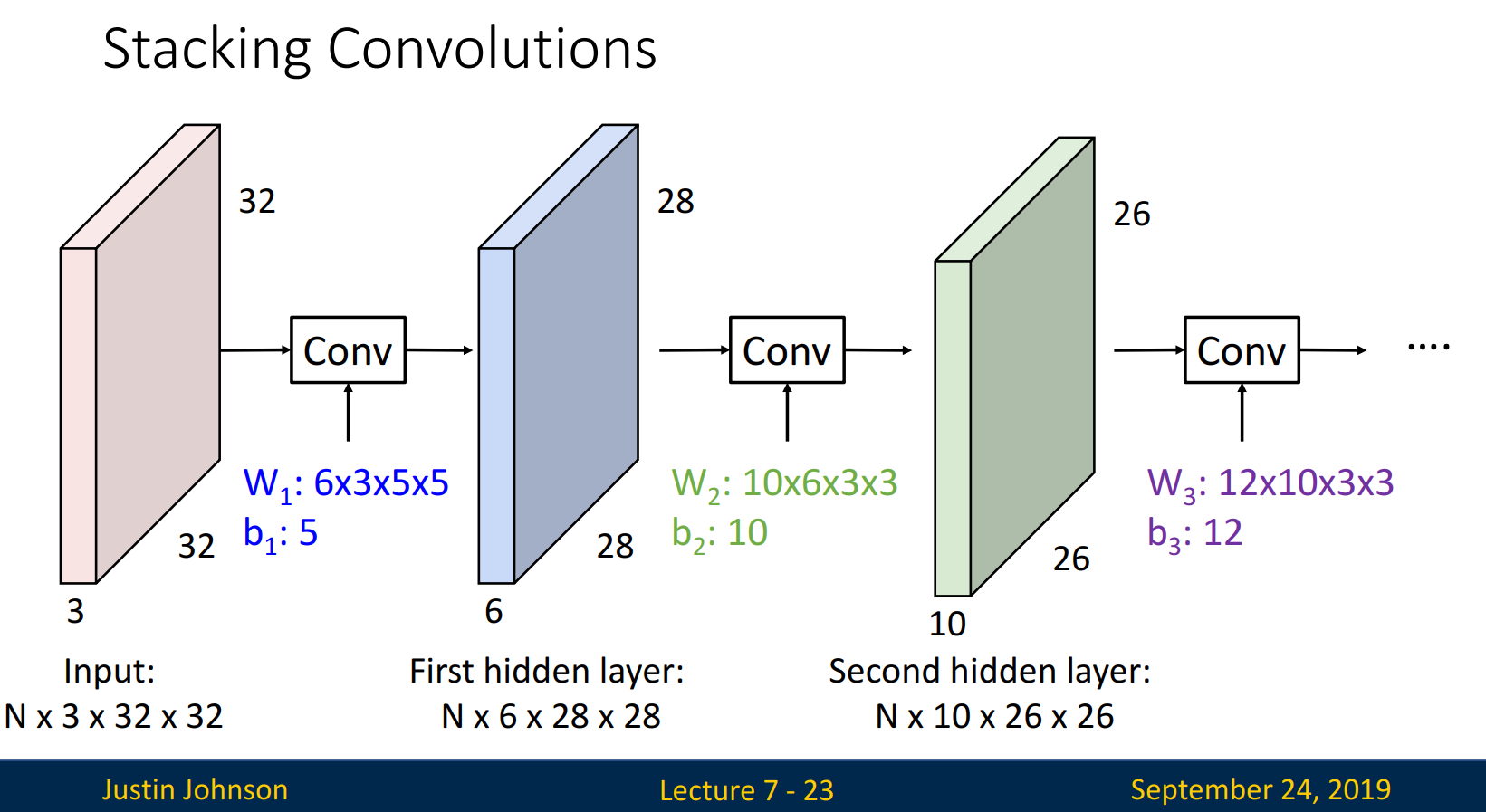
Input(N x 3 x 32 x 32)에서 First hidden layer(N x 6 x 28 x 28)로의 과정을 통해 stacking을 설명하겠습니다. N은 batch로 항상 동일한 값을 지니고, hidden layer의 depth는 # of filter(= # of activation map)로 설정됩니다. width & height는 계산식을 통해 계산됩니다.
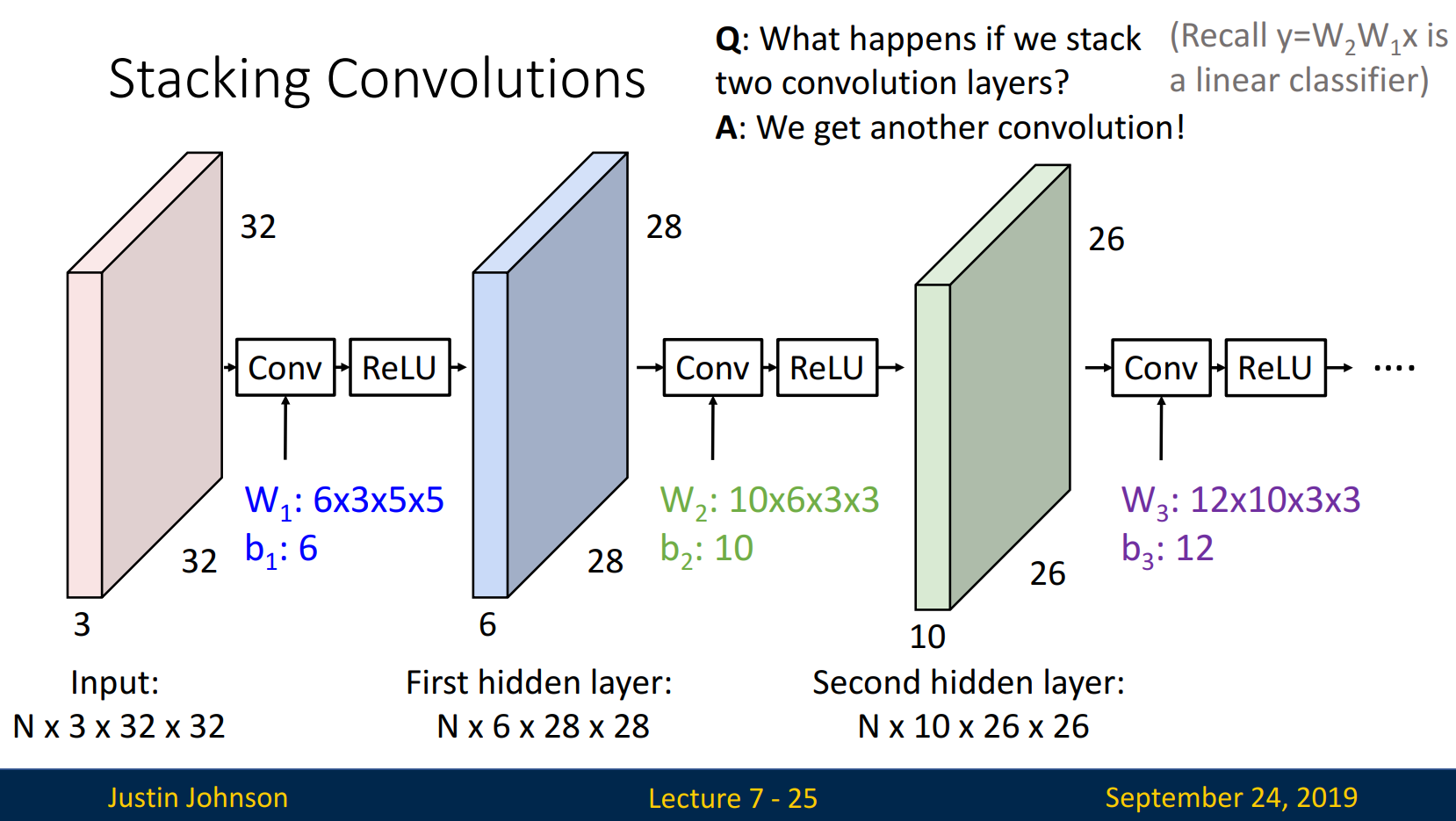
Q. What happens if we stack two convolution layers?
A. We get another convolution!
Covolution layer를 두 개 쌓는다고 두 개 층의 효과가 발휘될까요? 단지 다른 convolution을 얻을 뿐, 여전히 한 개 층의 효과를 보입니다. 활성화함수를 배울 때 살펴본 것처럼, 활성화함수(ex. ReLU)를 통해 비선형 변환을 진행합니다.
What filters learn
Filter가 어떻게 '학습'하는지 살펴보겠습니다.
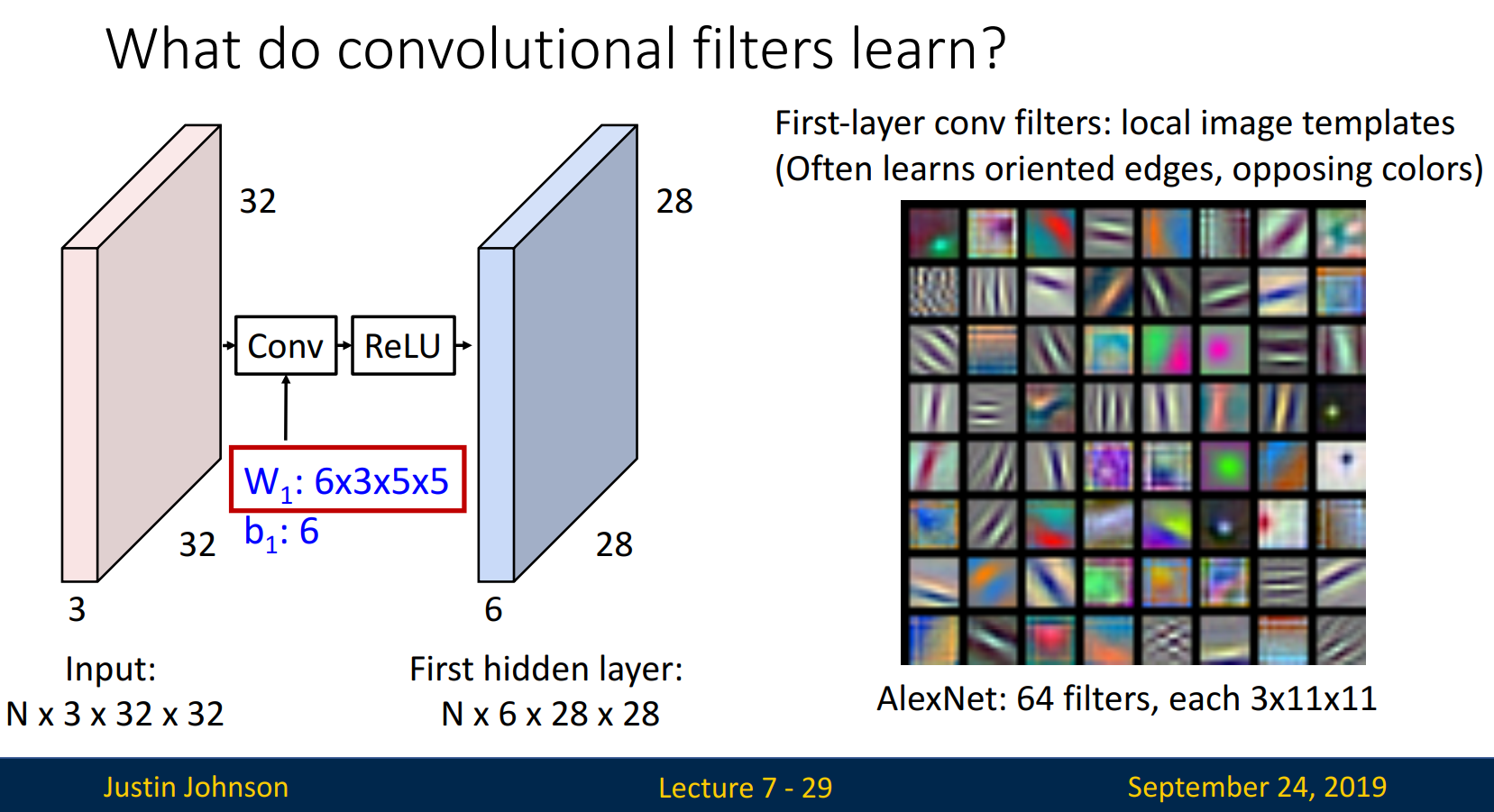
우측 그림은 3x11x11 size를 가지는 64개의 filter를 보여줍니다. filter에는 edge, 상반되는 색이 입력되어 있고, 이미지의 특징을 잘 인식하는 쪽으로 학습합니다.
그럼 연산은 어떻게 진행될까요?
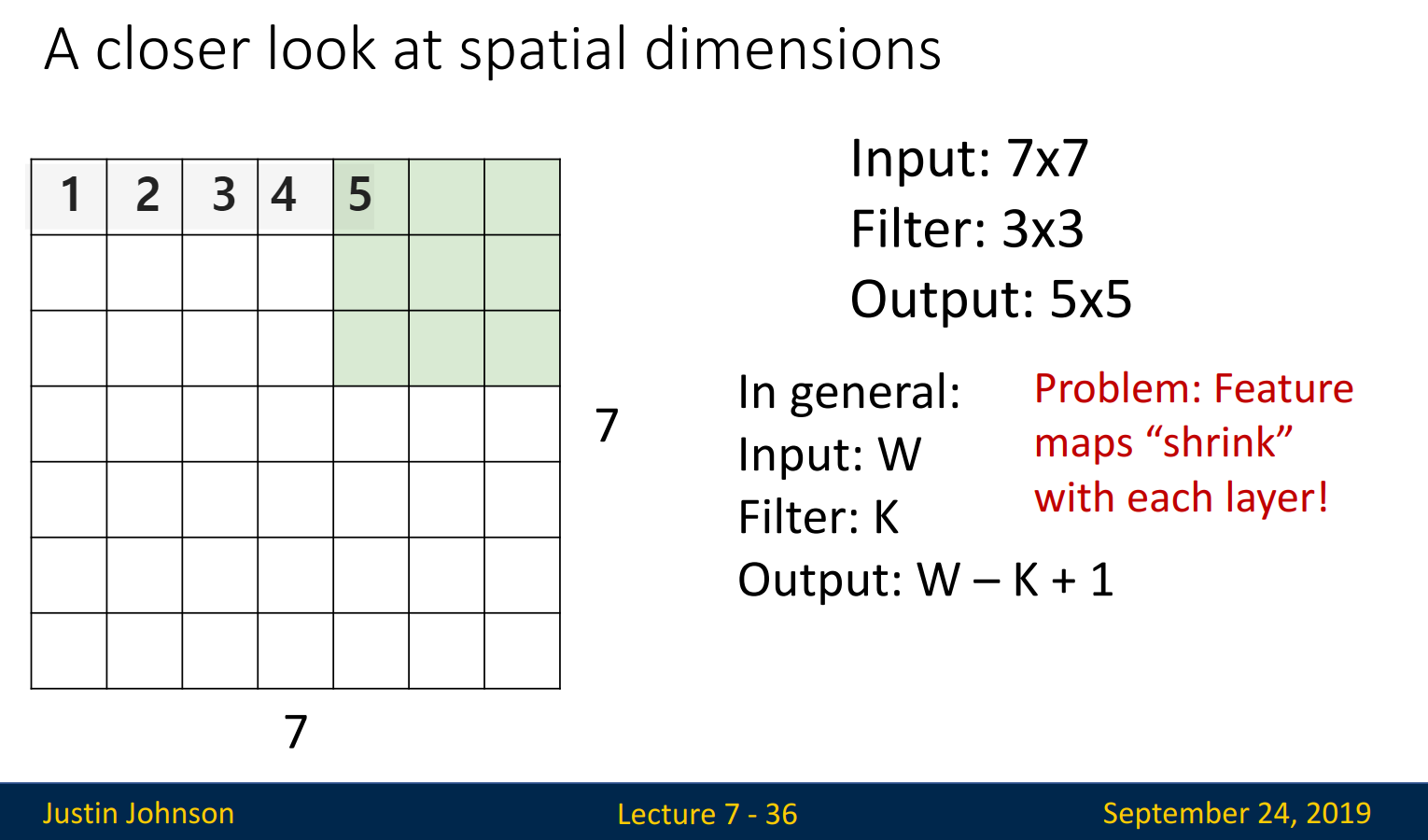
Input size가 7 x 7, filter size가 3 x 3이면, 가로로는 3 x3 filter가 5번 이동할 수 있습니다. 맨 좌측을 1, 맨 우측을 7이라고 한다면, 5까지 이동한 후에는 더 이상 이동할 수 없기 때문이지요(filter의 가로가 3이기 때문). 세로로도 마찬가지로 이동하기에, output size는 5 x 5가 됩니다. 계산식으로 표현한다면, (Input - Filter + 1)로 표현할 수 있습니다. 하지만 이 계산식을 사용하면 문제가 발생합니다. 처음 Input은 7 x 7인데, 다음 layer에서는 5 x 5가 input으로 사용되고, 그 다음은 3 x 3이 될 것입니다. 즉 layer를 거칠 때마다 Input size가 줄어드는 문제가 발생합니다.
Padding
Padding은 Layer를 지날때마다 size가 줄어드는 문제를 해결하고자 사용합니다.
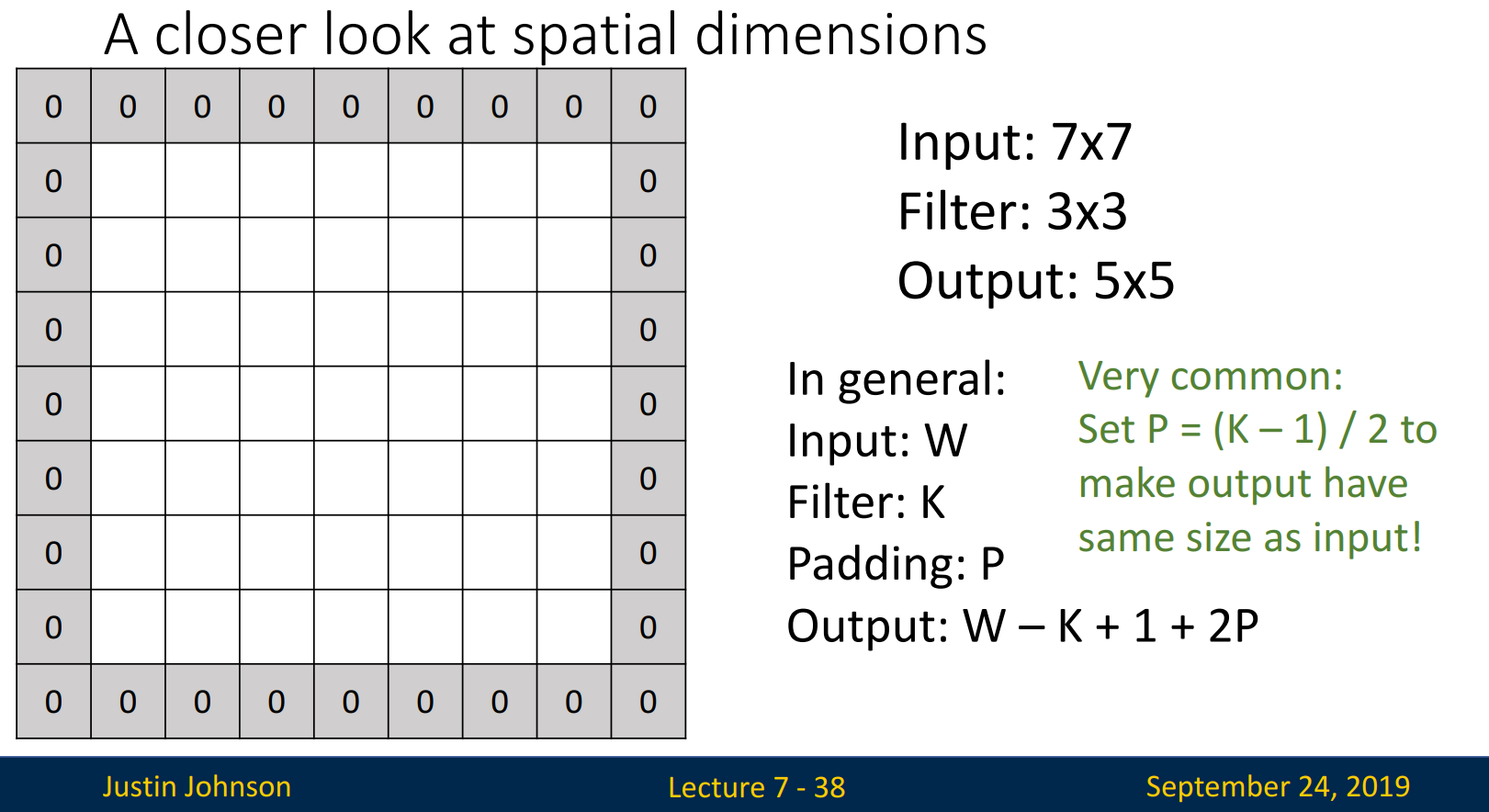
Edge에 zero를 padding한다면 더 이상 size가 줄어들지 않습니다. 이전에 제시된 계산식 (Input - Filter + 1)로 예를 들자면, 기존에는 (7-3+1=5)인데, padding을 추가한다면 Input size가 9 x 9가 되기에 (9-3+1=7)로 실제 Input size인 7 x 7이 보존됩니다. 따라서 Padding을 추가한 계산식은 (Input - Filter + 1 + 2 x Padding)이 됩니다.
*추가로 일반적으로 Input size와 output size를 똑같이 만드는 Same Padding을 진행하기에, P = (k-1) / 2로 Padding의 크기를 결정합니다. 예시에서 k=3이기에 P=1로 설정하였습니다.
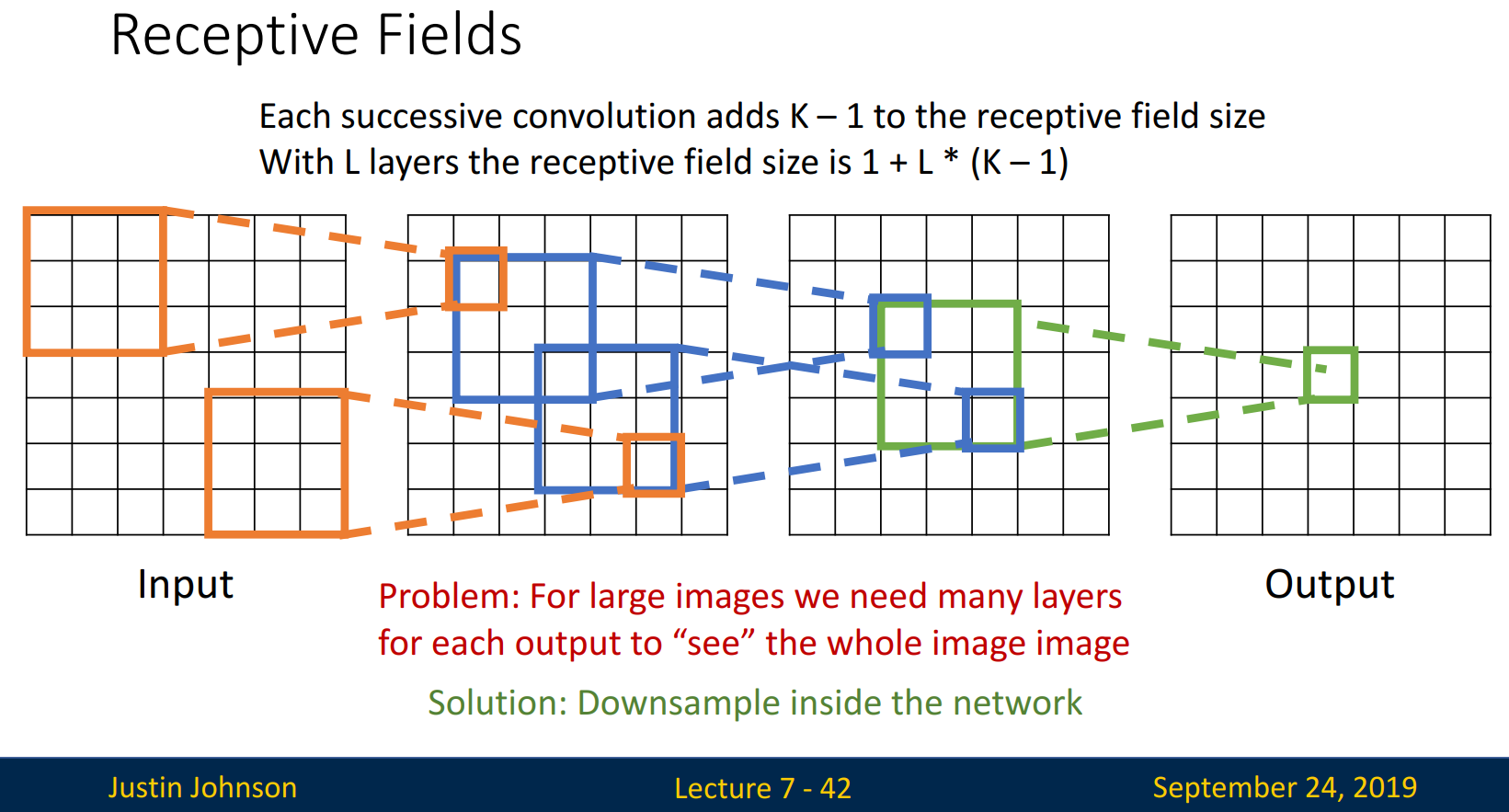
Convolution을 사용하는 이유는 파라미터 수를 줄이기 위함입니다. 위 그림에서 볼 수 있듯이 Convolution을 반복할수록 파라미터는 줄어들어, 최종적으로 1개까지 압축가능합니다.
padding을 추가하지않은 Input(size: 7 x 7)에 filter(size: 3 x 3)을 Convolution 하면, 5 x 5로 줄어든 output이 나옵니다. → 다음 Convolution에서는 3 x 3 → 최종적으로 1 x 1로 압축되게 됩니다. 테두리들을 하나씩 뺀다고 생각해도 되겠네요.
작은 size의 이미지는 상관없지만, 큰 size 이미지에서는 1 x 1에 도달하기까지 많은 layer가 요구된다는 문제가 생깁니다. 일반적으로 이미지의 크기는 매우 크니까요.
Stride
Stride로 큰 사이즈의 이미지는 많은 layer가 요구되는 문제를 해결할 수 있습니다.
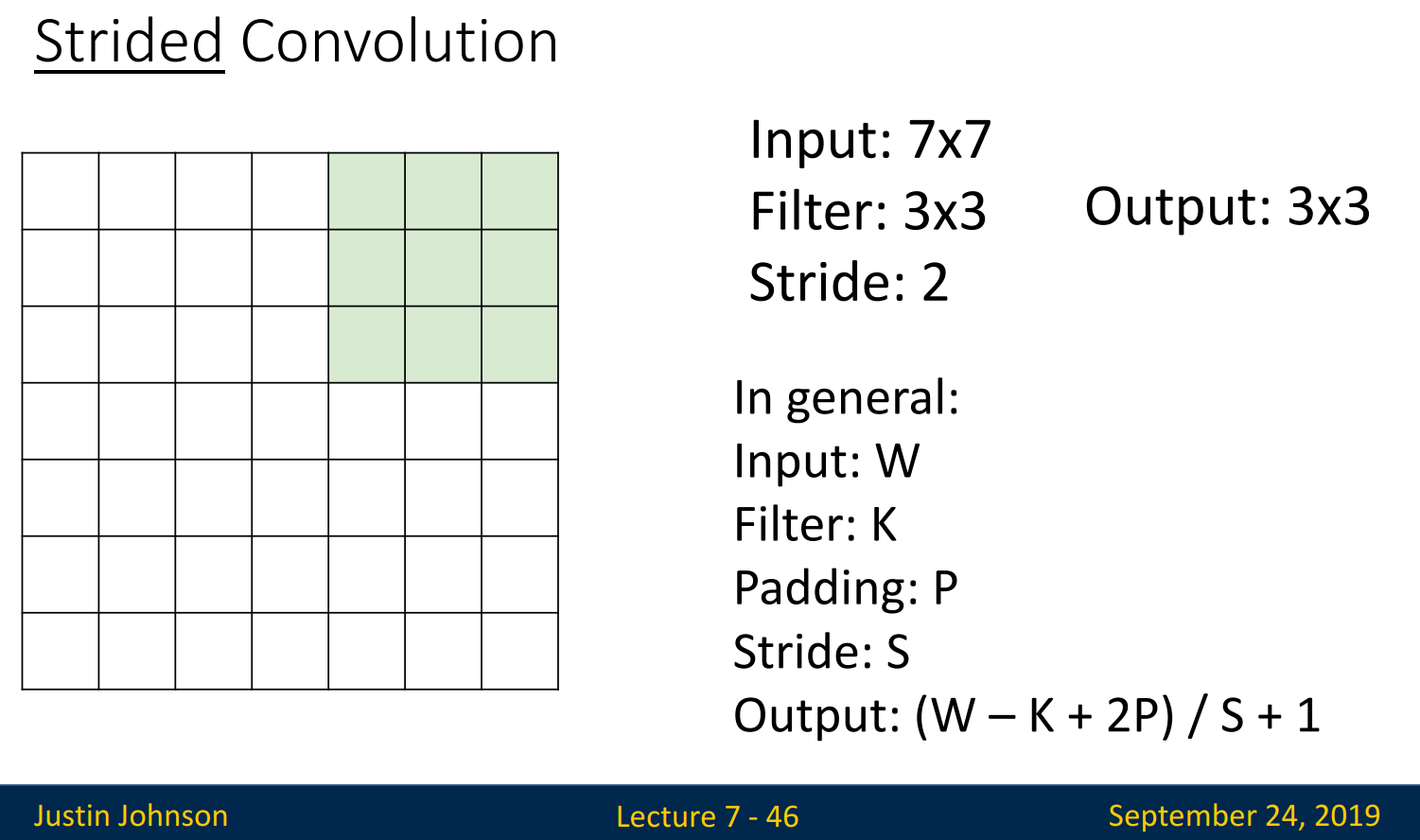
Filter가 한 칸이 아니라 두 칸, 세 칸씩 이동한다면 Output size가 빠르게 줄어들고, 적은 layer가 필요할 것입니다. 몇 칸을 이동할 것인가가 Stride입니다. 최종적인 계산식은 다음과 같습니다.
(Input - Filter + 2 x Padding) / Stride + 1
지금까지 배운 Convolution을 요약하면 다음과 같습니다.

Pooling
Stride 외에도 downsampling을 하는 방법이 존재합니다. 바로, Pooling입니다.
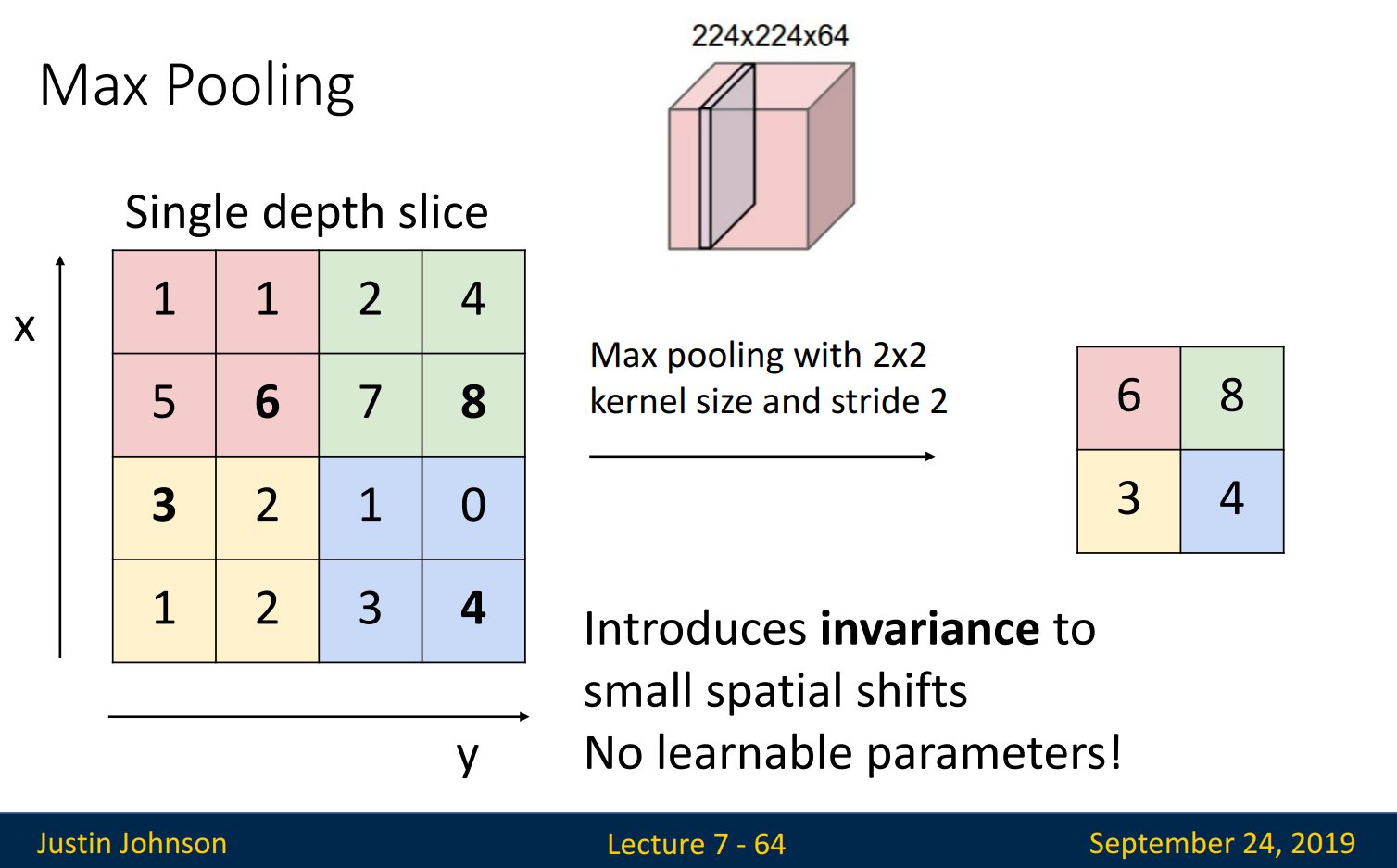
- Pooling은 Convolution layer를 거치고 만들어진 activation map(= feature map)에서, 특정 영역의 정보만을 사용하여 downsampling 하는 방법 → Activation map이 줄어드는 효과 → 파라미터 수가 줄어듬
- 종류: 영역의 가장 큰 값을 사용하는 Max Pooling(주로 사용), 영역의 평균값을 사용하는 Average Pooling
- Pooling은 활성화 함수의 역할(비선형 변환)도 하기에, Pooling을 하면 활성화 함수를 사용하지 않아도 상관없음
CNN의 구조를 잠시 정리해 볼까요?
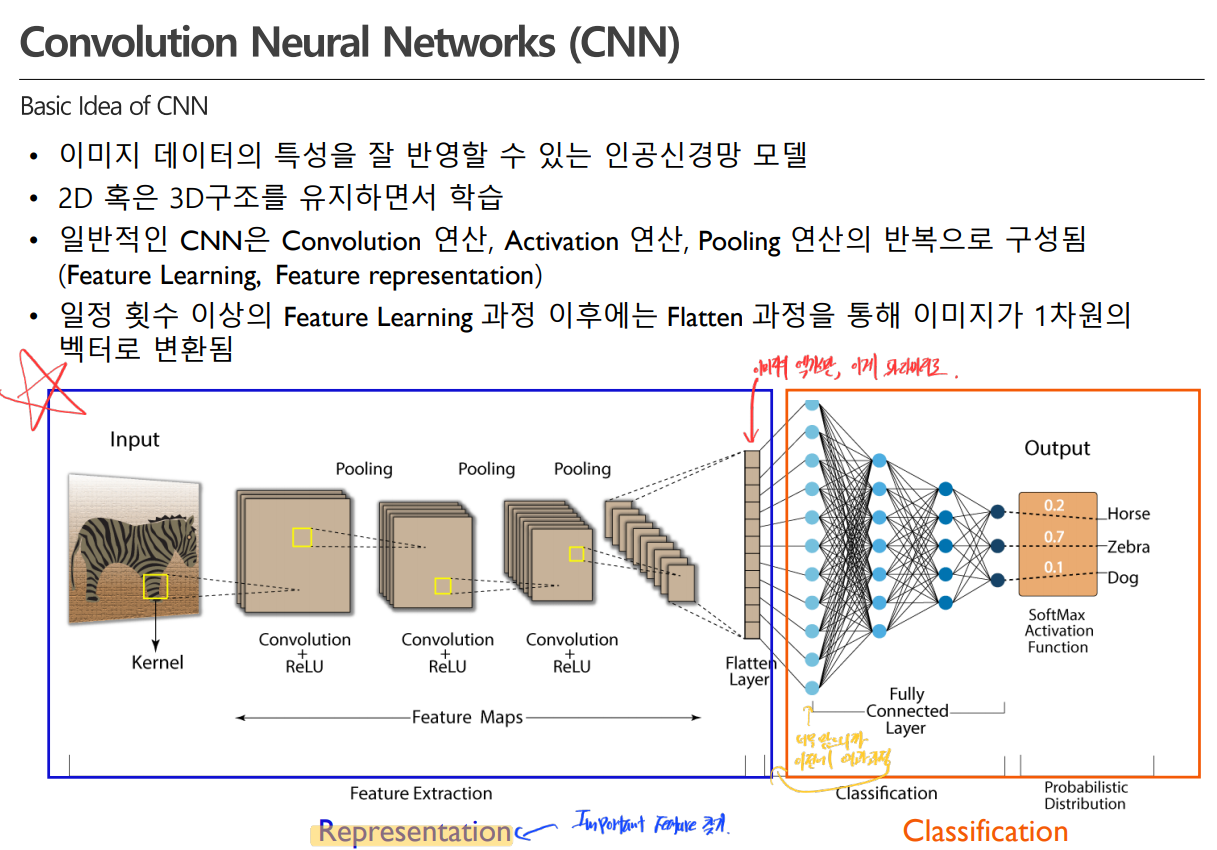
CNN은 크게 Representation과 Classification으로 이루어집니다. Representatinon은 중요한 Feature를 찾는 단계이고, Classification은 일반적인 인공신경망 학습 단계입니다.
1. Representation: (Convoution→Activation→Pooling) → (Convoution→Activation→Pooling) →...
2. Flattening: N차원 → 1차원 벡터로 변환 / 두 번째 단계의 Input 형식에 맞추기 위해서 변환
3. Classification: 순전파 → 역전파 → 순전파 → 역전파 →...
N-D Convolution
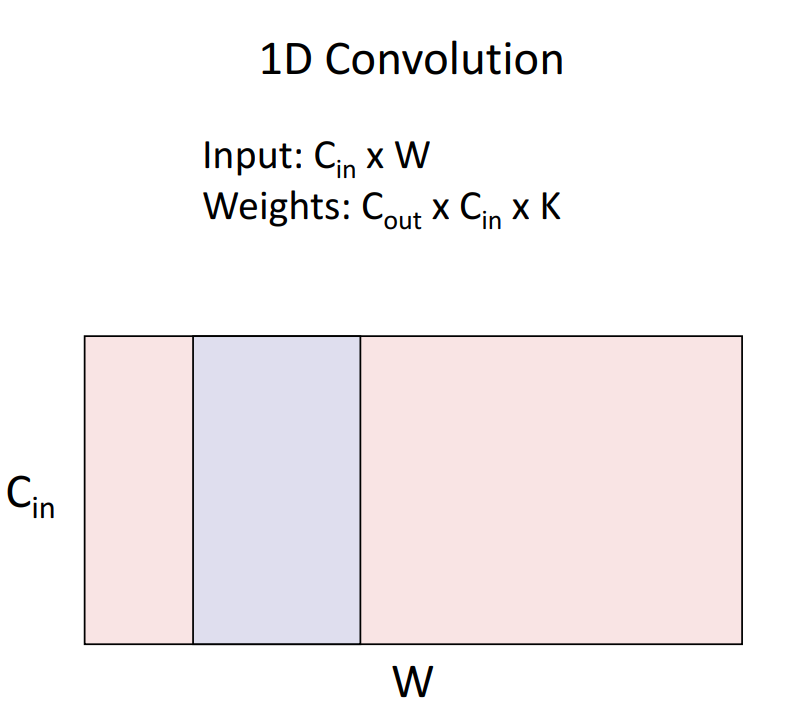
1D Convolution은 시계열에서 주로 사용됩니다. 자연어, 오디오 데이터 또한 시계열처럼 표현가능하기에 자연어, 오디오 데이터에도 사용됩니다. 1D Convolution은 1x1 연산을 수행하여 # of filter( = # of activation map = # of channel)를 감소시켜 연산량을 현저하게 줄입니다.
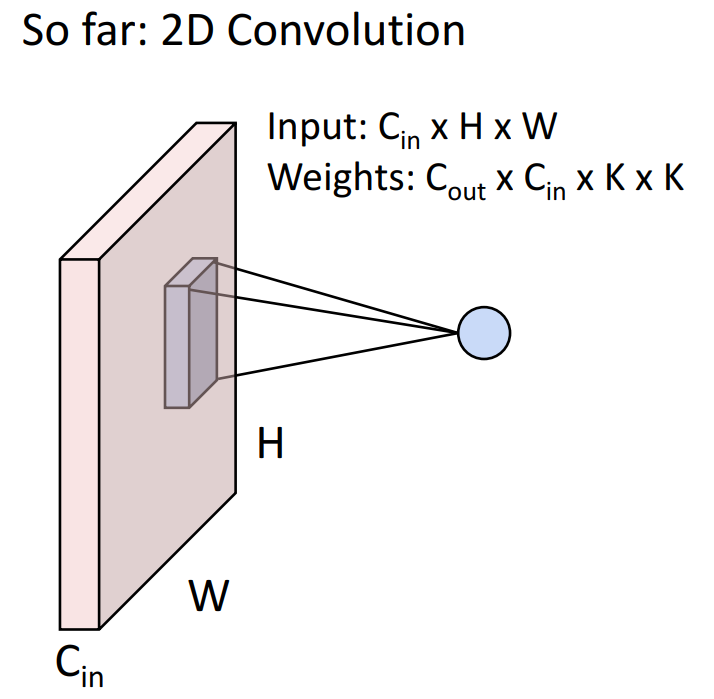
2D Convolution은 이미지 데이터에 사용됩니다. 이번 강의에서 살펴본 Convolution입니다.
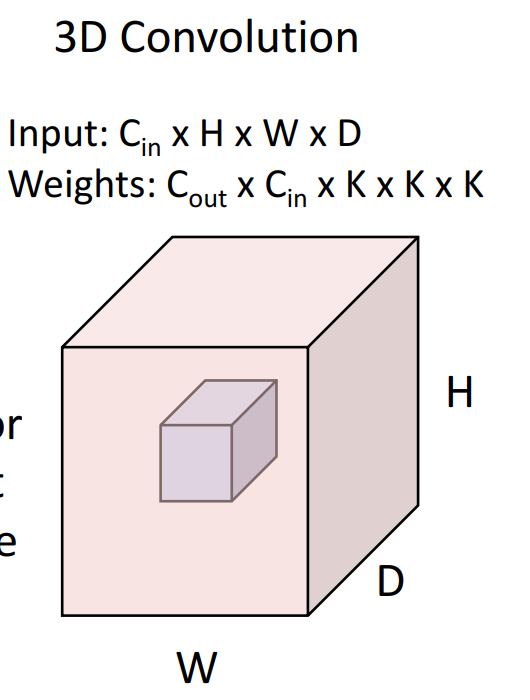
3D Convolution은 MRI, 비디오와 같은 3D 이미지 데이터에 사용됩니다.
Batch Normalization
Q. Deep Networks very hard to train! → A. Normalization

Batch Normalization은 Fully Connected 혹은 Convolutional layers를 지난 후 만들어진 output을 (평균=0, 공분산=단위행렬)로 정규화시켜주는 것입니다. internal covariate shift는 layer 마다 input의 분포가 달라지는 것을 말하고, 이는 정확한 학습을 방해합니다. 따라서 internal covariate shift 해결과 optimization을 향상하기 위해 Batch Normalization을 사용합니다.

Batch의 데이터 수를 N, 차원을 D라고 할 때 각 차원별 평균과 분산으로 normalization을 수행합니다. 이때 training data 전체를 학습하는 대신, 일정 크기에 해당하는 minibatch로 진행합니다.
Problem: What if zero-mean, unit variance is too hard of a constraint?
만약 평균 0, 분산 unit variance로 normalization 하기 어렵다면 어떻게 할까요?

Shift parameter 감마, 베타를 이용하여 이를 해결합니다.
Problem: Estimates depend on minibatch; can’t do this at test-time!
하지만 추정치가 minibatch에 의존하기에 test-time에서는 사용할 수 없습니다. → training data의 평균과 분산을 test에서 활용합니다.

Fully-connected network & Convolutional network 모두 Batch Normalization을 사용할 수 있습니다. 차이점은 convolutional network spatial dimension도 고려한다는 점입니다.
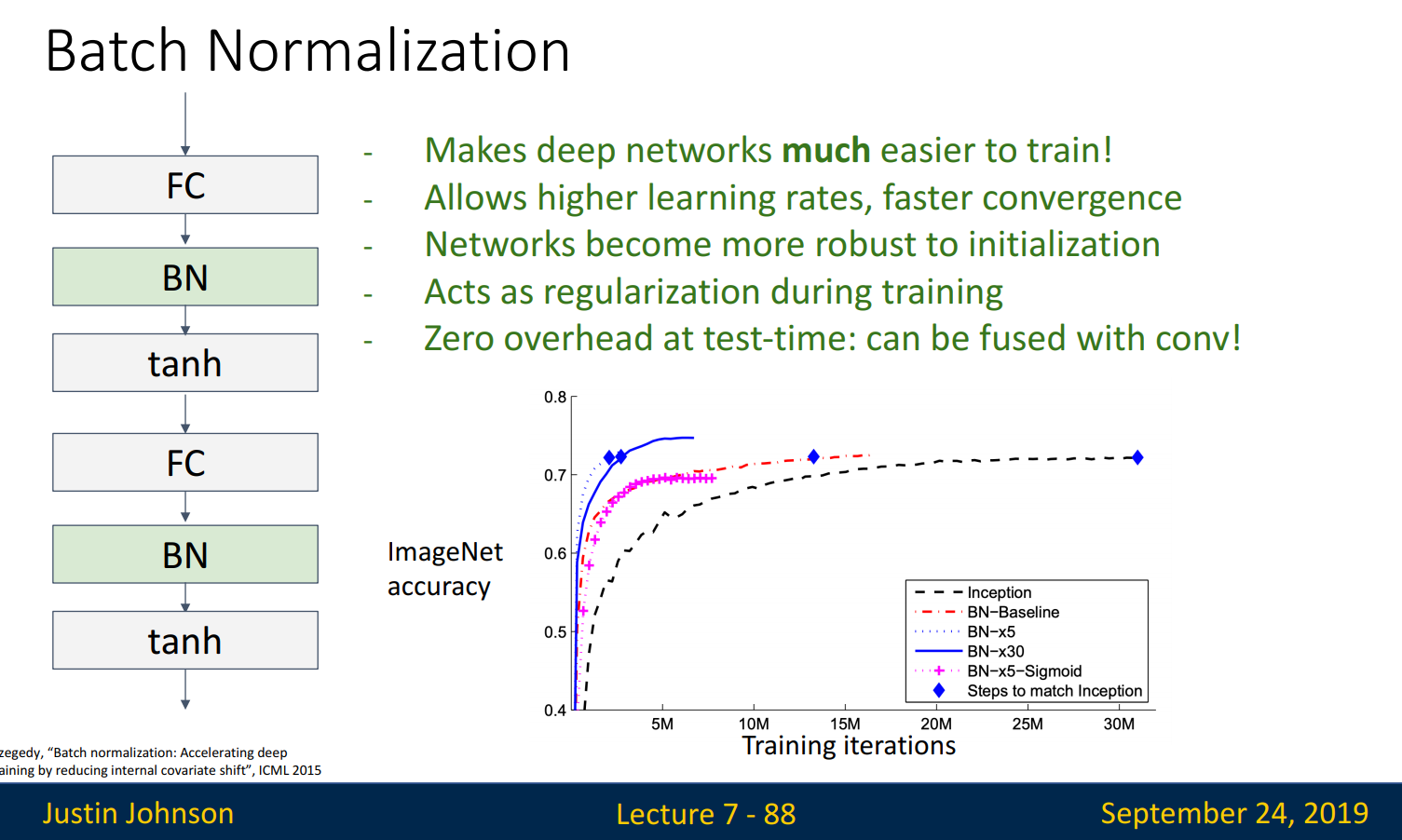
Batch Normalization은 Fully Connected 혹은 Convolutional layers 다음, 활성화 함수 이전에 수행됩니다. Batch Normalization의 장점은 다음과 같습니다.
- Deep network의 학습을 쉽게 해 주고, 학습률을 높이고 빠르게 수렴하도록 함
- Network 초기화에 Robust(강건한)함
- 학습 중 정규화의 효과를 보여줌
물론 단점도 존재합니다.
- 이론적으로 이해하기에 어려움이 있음
- training과 testing에서 다르게 행동하기에 버그의 원인이 될 수 있음

Layer Normalization은 평균과 분산을 batch dimension이 아닌, feature dimension에 대해서 계산하기에 train과 test에서 똑같은 양상, 즉 test-time에서 사용가능합니다.
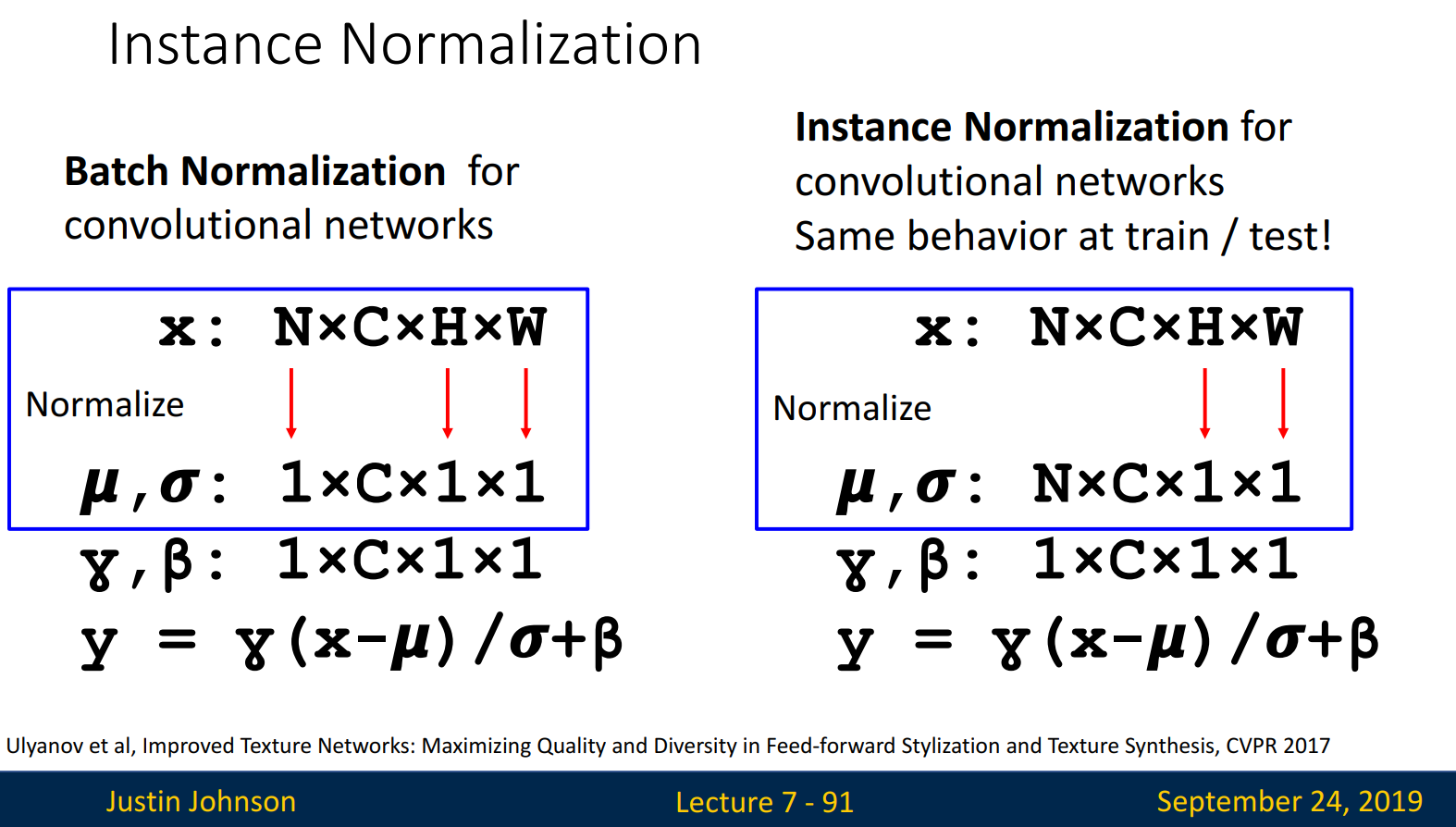
Instance Normalization은 평균과 분산을 spatial dimension에 대해서 계산합니다.
정리하면 다음과 같습니다.
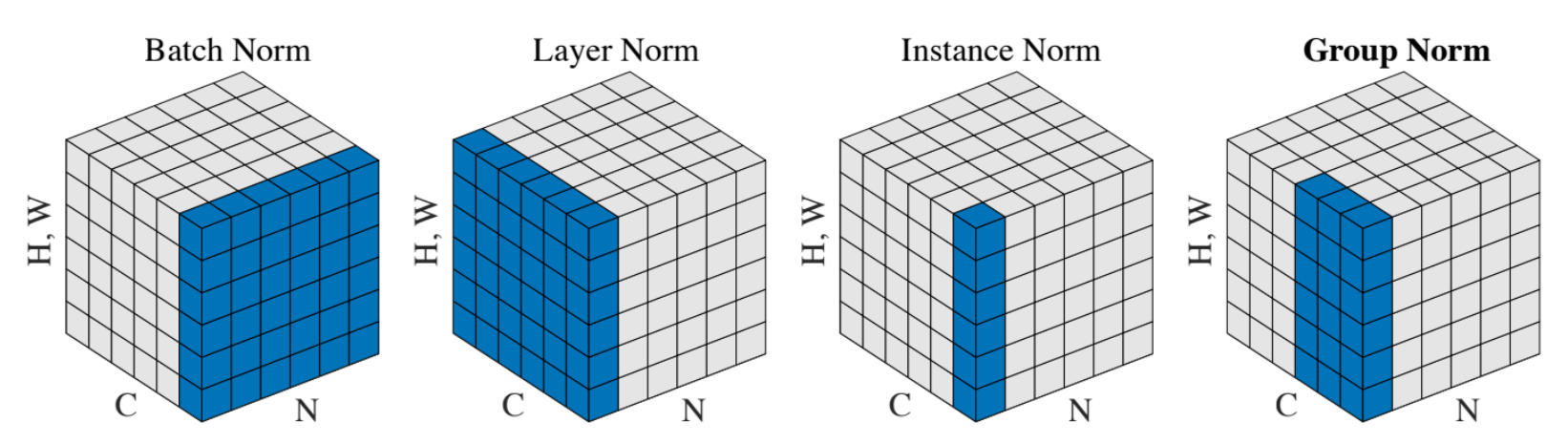
- Batch Norm: Batch, Spatial dimension
- Layer Nrom: Spatial, Channel dimension
- Instance Norm: Only Channel dimension
- Group Norm: Different subset of Channel dimension
자료 작성에 참고한 블로그입니다.
https://towardsdatascience.com/understanding-1d-and-3d-convolution-neural-network-keras-9d8f76e29610
Understanding 1D and 3D Convolution Neural Network | Keras
When we say Convolution Neural Network (CNN), generally we refer to a 2 dimensional CNN which is used for image classification. But there…
towardsdatascience.com
11-02 자연어 처리를 위한 1D CNN(1D Convolutional Neural Networks)
합성곱 신경망을 자연어 처리에서 사용하기 위한 1D CNN을 이해해보겠습니다. ## 1. 2D 합성곱(2D Convolutions) 앞서 합성곱 신경망을 설명하며 합성곱 연산…
wikidocs.net
[개념 정리] Batch Normalization in Deep Learning - part 1.
딥러닝을 공부하다 보면 자주 접하는 이론적인 내용이자 실제 구현에서도 라이브러리를 이용하여 쉽게 Layer로 추가하여 사용하는 Batch Normalization에 대해 알아보자. 개요 ICML 2015에 한 논문이 등
cvml.tistory.com
'공부 정리 > Machine learning & Deep learning' 카테고리의 다른 글
| [EECS 498-007 / 598-005] Lecture 11: Training Neural Network (0) | 2023.02.01 |
|---|---|
| [EECS 498-007 / 598-005] Lecture 8: CNN Architectures (0) | 2023.01.26 |
| [EECS 498-007 / 598-005] Lecture 6: Backpropagation (0) | 2023.01.17 |
| [EECS 498-007 / 598-005] Lecture 5: Neural Network (2) | 2023.01.11 |
| [EECS 498-007 / 598-005] Lecture 4: Optimization (0) | 2023.01.08 |



