- 본 게시글은 Justin Johnson 교수님의 Deep Learning for Computer Vision, University of Michigan 정리글입니다.
- 개인적인 생각이 서술되어 있습니다. 잘못된 내용이 존재할 확률이 존재하기에 주의 바랍니다.
- 잘못된 내용, 오타는 지적해주시면 감사하겠습니다.
강의링크:
https://www.youtube.com/watch?v=YnQJTfbwBM8&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=4
강의자료:
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture04.pdf
4.1. Optimization

머신러닝에서 최적화란 loss function을 minimize(최소화)하는 파라미터 W를 찾는 것입니다.
Random Search
Random Search는 말 그대로 Random하게 만든 W에 대해서 loss 값들을 구합니다.
생성된 loss 중 가장 작은 best loss를 찾습니다.
말 그대로 Random한 방법이니 어렵지 않습니다. 만약 성능이 좋다면 가장 좋겠지요.!
하지만 SOTA(현재까지 알려진 가장 좋은)의 정확도가 95%인데 반해,
Ranom Search의 정확도는 15.5%에 불과합니다.
Numerical Gradient (Follow the Slope)

위 식은 고등학교 미적분 시간에 많이 본, 1차 도함수입니다. multimple(2차원 이상) 차원에서는 gradient가 편미분 벡터로 표현됩니다.
*1차 도함수의 미분은 일정한 상수(스칼라)이지만, 2차원부터는 아니기 때문입니다.
방향의 기울기는 방향 & gradient의 내적값이고, 가장 가파른 descent(내리막) 방향은 음의 gradient입니다.
* -max → +min
Loss는 다음과 같은 방법으로 계산됩니다.
- 현재 W의 loss와 각 차원에서 h만큼 이동한 때의 loss 차이를 계산합니다. f(x + h) - f(x)
- 차이를 h로 나누어 gradient(변화)를 계산합니다. f(x + h) - f(x) / h
- 위 두 단계를 모든 차원에 대해 반복합니다 (1차원, 2차원 등, 아래의 그림은 3차원의 loss 계산).
*10차원이면 10번 반복하겠죠?

이러한 Numerical Gradient는,
1. Slow
아주 작은 h의 gradient를 계산하고, 이를 모든 차원에 대해 계산합니다. 따라서 매우 느립니다. 시간 복잡도 Big-O로 표현하면 O(n)입니다. Input이 증가할수록 시간복잡도는 이에 비례하여 증가합니다.
2. Approximate
대략적인 값을 산출하기에, 추천되는 방법은 아닙니다.
Analytic Gradient
Calculus(미적분)를 활용하여 analytic gradient를 계산합니다.
Analytic Gradient는 dL / dW, loss function을 W에 대해 미분한 값을 계산합니다.

Analytic Gradient 정확하고, 빠릅니다. Numerical Gradient의 단점이 모두 극복되었지요.
하지만 error-prone(오류를 발생하기 쉬운)하기에 실제로 사용하기 전에 Numerical Gradient를 통해 검증합니다. 이를 gradient check라고 부릅니다.
4.2. Gradient Descent
Gradient Descent(경사 하강법)의 기본 개념은 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것입니다. (위키백과 참조)
Hyperparmeters는 다음과 같습니다.*Hyperparameters: 사용자가 직접 설정해주는 값
- Weight initialization method
- Number of steps
- Learning rate
Number of steps, Learning rate는 사용자의 computing power에 따라 알맞게 설정하면 됩니다. 하지만 Learning rate가 너무 작거나 크면, 학습이 안되거나 학습이 잘못될 확률이 있습니다.
Gradient Descent의 목적은 기울기가 0에 가까운 빨간 쪽으로 가는 것입니다 (등고선을 떠올리면 이해에 도움이 될 것 같습니다). 그렇기에 W가 어디서 시작했는지에 따라 학습 시간, 효율이 달라지겠죠?

Batch Gradient Descent
Batch Gradient Descent는 가장 기본적인 경사하강법입니다. 모든 loss를 합하기에 N이 커질수록 비용이 증가합니다.
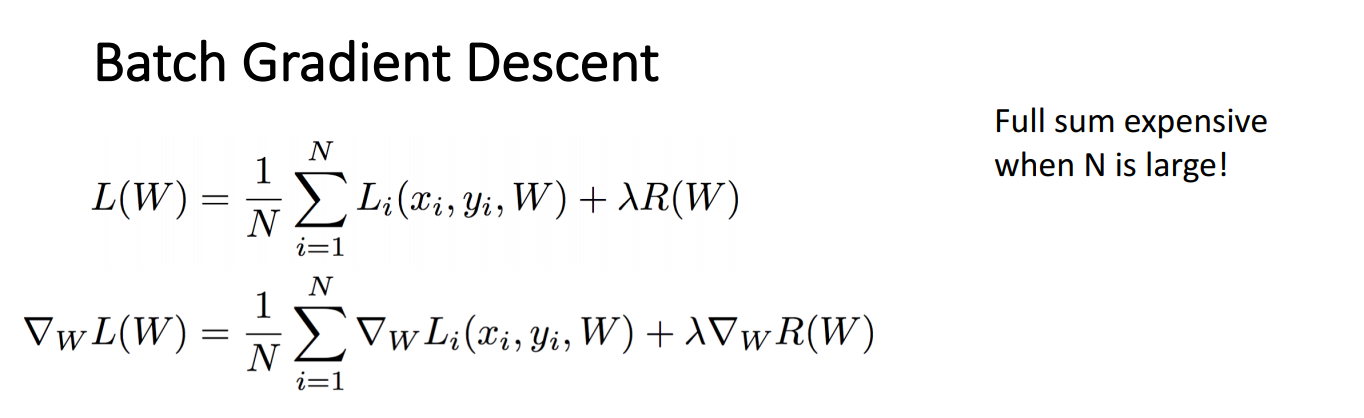
Stochastic Gradient Descent (SGD)
Batch Gradient Descent의 비용 증가 문제를 해결하기 위해 SGD가 등장하였습니다.
SGD는 minibatch를 활용, 데이터의 일부분만 사용하여 gradient를 계산합니다.
Minibatch size는 일반적으로 32 / 64 /126처럼 2의 승수를 사용합니다.
SGD는 데이터 전체가 아니라 데이터의 일부분(minibatch)만 사용하기에,
표본의 분포가 모집단의 분포와 최대한 유사하게 표본을 추출하여야 합니다.
* 표본이 모집단을 대표할수록 정확하겠죠?

Hyperparmeter는 기존의 3개에 2개가 추가되었습니다.
- Batch size
- Data sampling
표본이 클수록 모집단과 가까워지기에, compution power가 허용가능한 범위에서 Batch size는 클수록 좋습니다.
Gradient Descent에 대해 잘 정리한 그림이 있어 이를 들고 왔습니다.
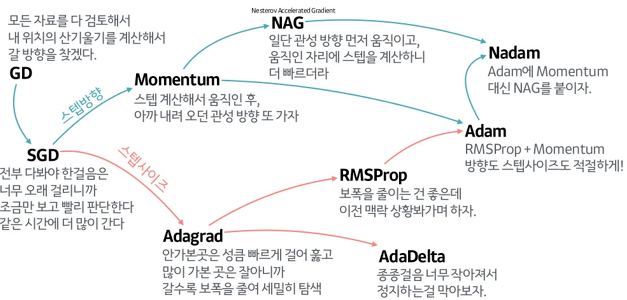
이미지 출처: https://wikidocs.net/152765
Problems with SGD
하지만 SGD에도 몇 가지 문제가 있습니다. 여기서는 3가지 문제를 살펴보겠습니다.

- What if loss changes quickly in one direction and slowly in another?
What does gradient descent do?
Batch Gradient Descent는 직선으로 나아가는 반면, SGD는 지그재그 방향으로 진행되어 더 많은 시간이 소요되고 overshooting 문제도 생길 수 있습니다.
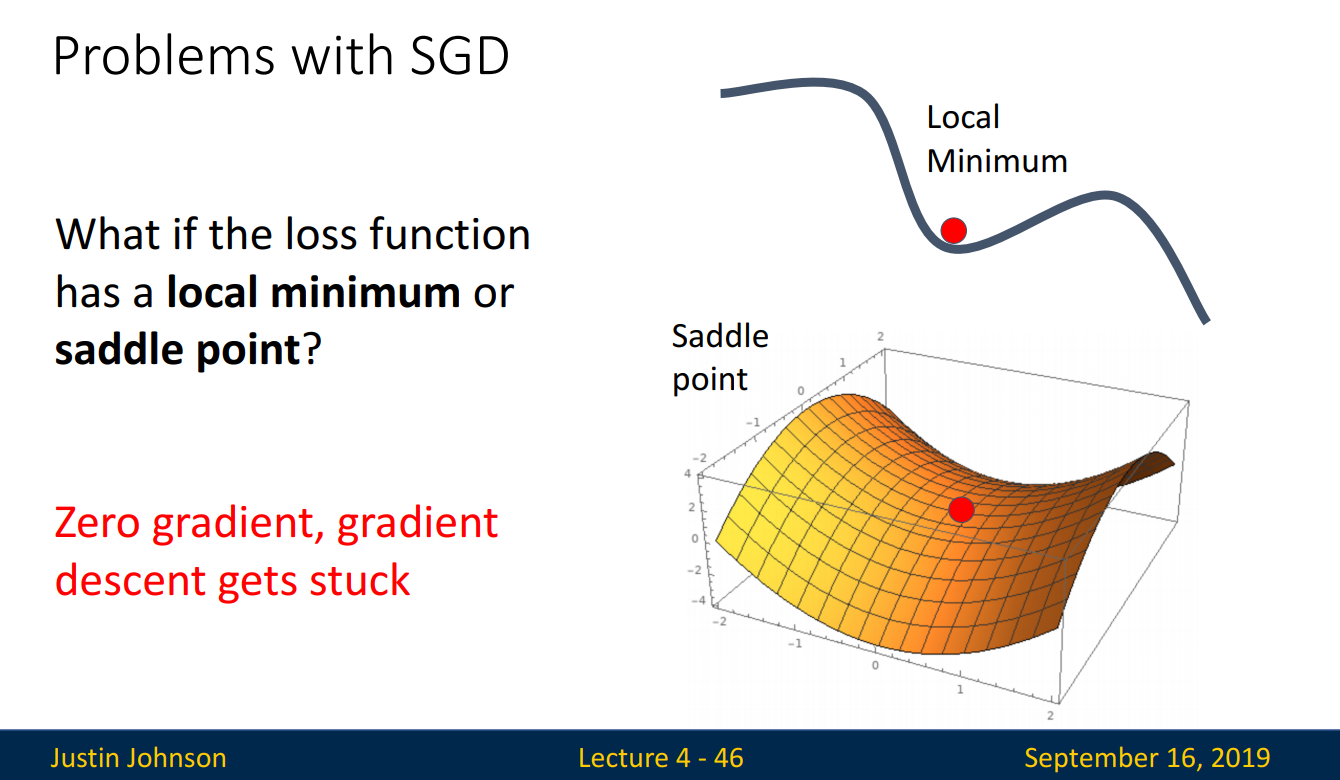
- What if the loss function has a local minimum or saddle point?
위에서 Gradient Descent의 목적은 기울기가 0에 가까운 쪽으로 이동하는 것이라고 언급하였습니다.
따라서 기울기가 0인 값을 만난다면 더 이상 학습을 하지 않겠지요.
만약 loss function이 2차원이라면 기울기가 0인 지점이 1곳이라 문제가 되지 않습니다. 하지만 차원이 커질수록 기울기가 0인 지점은 늘어나게 됩니다. Global Minimum은 언제나 1곳이기에, 이는 Local Minimum이 증가함을 뜻합니다. 즉, Optimal한 곳이 아닌 곳을 찾을 확률이 증가한다는 뜻입니다.!

SGD는 표본(Minibatch)을 사용하기에 loss function이 loss의 gradient를 완벽하게 따르지는 않습니다.
따라서 빨간색 쪽으로 가지 않고 다른 방향으로 돌아가는 등 Noise가 있는 경우가 많습니다.
그럼, SGD의 문제를 극복하는 방법을 알아보겠습니다.
SGD + Momentum
Momentum은 운동량, 가속도를 뜻합니다.
*운동량: 물체의 질량 x 속도

SGD는 지그재그로 움직이는 특성을 보이며, local minimum에 갇히는 경우가 많습니다. 만약 SGD에 운동량을 추가한다면 어떨까요?
속도는 벡터이므로 방향성을 지닙니다. 따라서 기존의 방향을 유지하는 경향이 생겨 지그재그 움직임이 줄어듭니다. 즉, 일정한 방향으로 이동하는 경향이 추가됨을 의미합니다. 이러한 효과로 SGD보다 더 빠르게 중심으로 이동가능합니다.

좌측의 그림은 SGD+Momentum으로 현재 위치의 Velocity에 Gradient를 결합하여 actual step(W)를 업데이트합니다.
v= rho * v + dw로 velocity + Gradient로 v를 업데이트한 다음,
w -= learning_rate * v로 W를 업데이트하는 위 식의 코드와 동일한 의미입니다.
우측의 그림은 Nesterov Momentum으로 Velocity를 먼저 이동한 다음, 그 위치에서의 Gradient를 결합하여 actual step(W)를 업데이트합니다. 왜 이런 방식을 활용할까요?
바로 '관성' 때문입니다.
Momentum은 관성을 지니기에 Optimal을 지나쳐갈 수 있는데 Nesterov Momentum은, 먼저 이동을 한 다음 그 위치에서 Gradient를 결합하기에 추후에 방향성을 결정할 수 있습니다. 따라서 적절한 지점에서 멈추는 효과를 발휘합니다.
*10일 전에 수요를 예측하는 것보다 5일 전에 수요를 예측하는 것의 정확도가 높을 것이라고 예상하는 느낌입니다.
수식으로 표현하면 다음과 같습니다.

옵티마이저들을 조금 더 살펴보겠습니다.
AdaGrad
AdaGrad(Adaptive Gradient)는 각 Feature별로 다른 learning rate를 적용합니다. steep(많이 변화한) 방향은 작게, flat(많이 변화하지 않은) 방향은 크게 설정하여 이동합니다.
*Feature별로 다른 특징을 보이기에, 동일한 learning rate를 적용하는 것은 효과적이지 않습니다.
grad_squared += dw * dw로 변화한 정도를 계산한 후 이를 역수를 취함을 통해(grad_squared.sqrt()) 변화의 정도가 클수록 제약이 생김을 확인할 수 있습니다. 학습이 많이 된 Feature는 learning rate를 작게, 학습이 적게 된 Feature는 learning rate를 크게 조절할 수 있습니다.
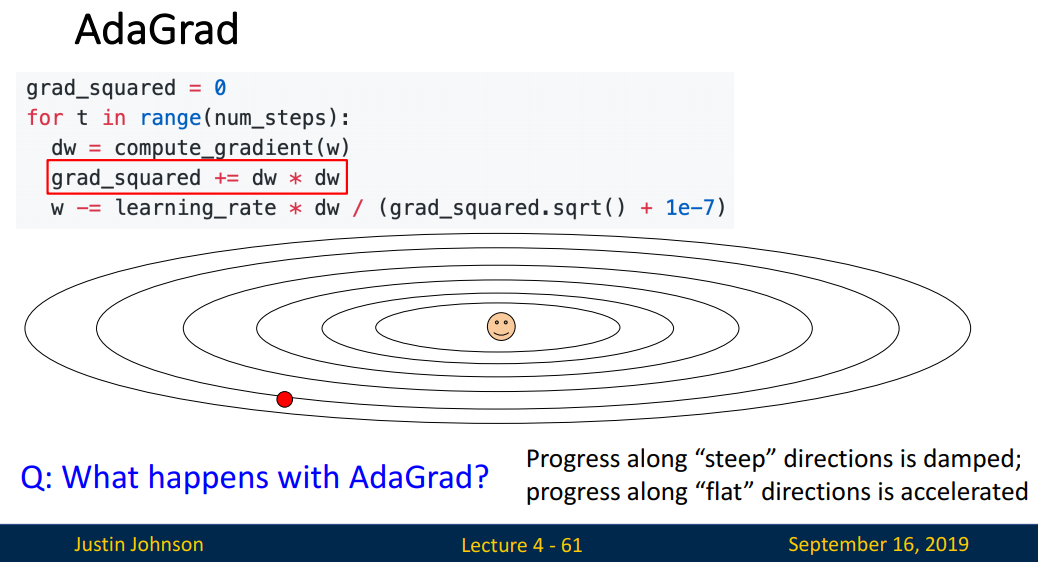
하지만 grad_squared += dw * dw로, 학습이 진행될수록 grad_squared는 커집니다.
* '+='는 누적합을 의미합니다.
값이 커질수록 이 역수는 0에 가까워집니다. 이는 더이상 학습이 진행되지 않을(그 자리에서 변화가 없음) 수 있는 문제를 지닙니다.
만약 Optimal에 도달하여 학습이 진행되지 않은 것이라면 좋겠지만, grad_squared가 너무 커져 학습이 진행되지 않은 것이라면 문제가 생깁니다. 이를 개선한 것이 RMSProp입니다.
RMSProp
RMSProp(Root Mean Square Propagation)는 AdaGrad와 마찬가지로 Feature별로 learning rate를 조절하지만, 방식에 차이가 있습니다.
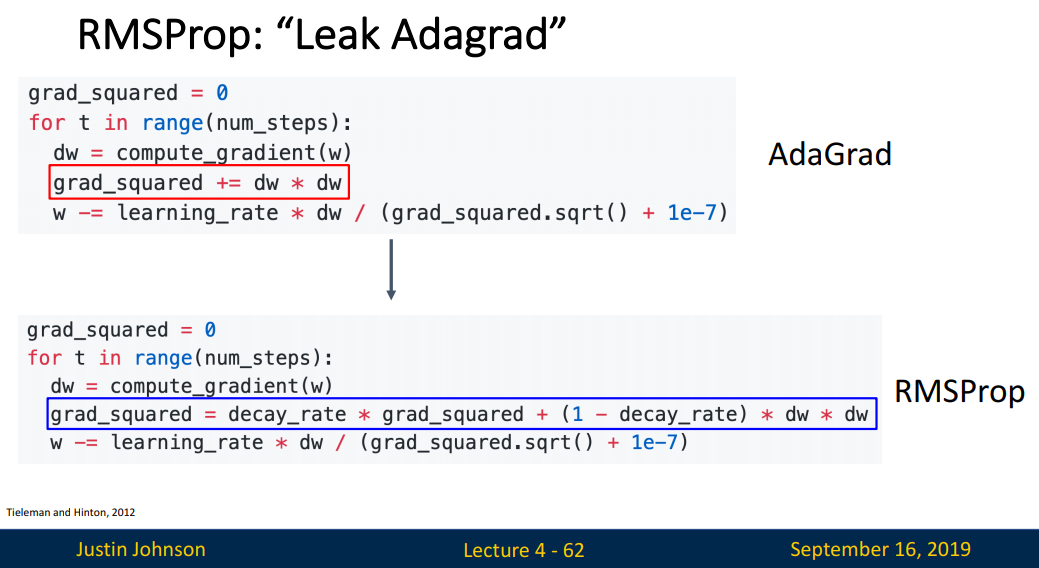
grad_squared = decay_rate * grad_squared + (1-decay_rate) * dw * dw에서 두 가지를 확인할 수 있습니다.
- 지수이동평균(EMA)으로 시간에 따른 비율을 조절하여 반영합니다.
- 누적합(+=)을 사용하지 않기에 시간에 따라 학습이 되지 않는 문제를 극복합니다.
Adam
Adam(Adaptive Mement Estimation)은 이름에서 유추가능하듯 RMSProp + Momentum의 효과를 보이는, 가장 대중적인 옵티마이저입니다.

코드의 moment1, moment2을 통해 Momentum, RMSProp 특징을 확인할 수 있습니다. 여러 논문을 통해 beta1 = 0.9, beta2 = 0.999가 가장 좋은 값이라고 알려져있습니다.
지금까지 살펴본 옵티마이저들을 비교한 표입니다.
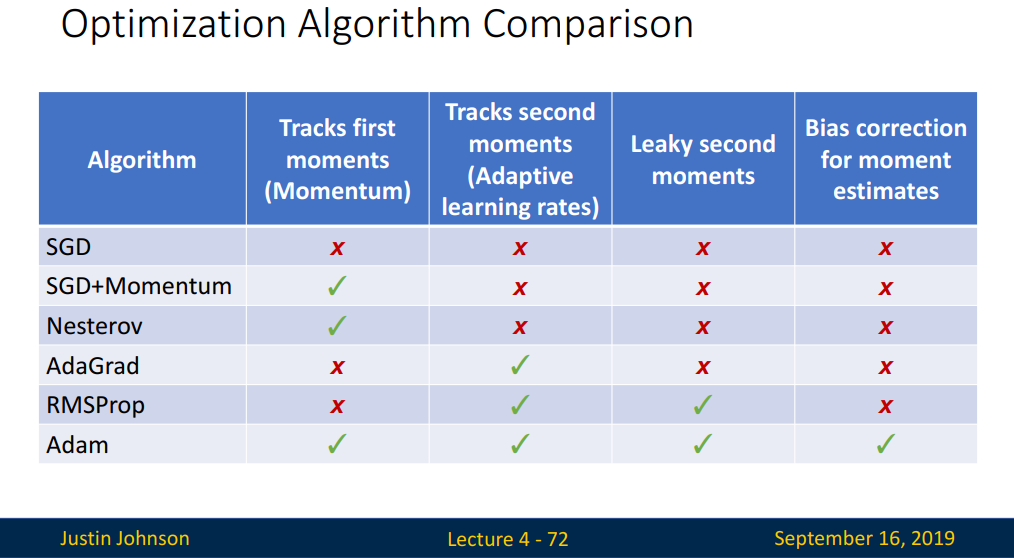
부족한 글을 읽어주셔서 감사합니다.
다음 강의로 찾아뵙겠습니다.
"유리병을 뛰어넘는 벼룩, 코끼리 사슬 증후군을 망각하는 인생을 만드세요"
'공부 정리 > Machine learning & Deep learning' 카테고리의 다른 글
| [EECS 498-007 / 598-005] Lecture 8: CNN Architectures (0) | 2023.01.26 |
|---|---|
| [EECS 498-007 / 598-005] Lecture 7: Convolutional Networks (0) | 2023.01.24 |
| [EECS 498-007 / 598-005] Lecture 6: Backpropagation (0) | 2023.01.17 |
| [EECS 498-007 / 598-005] Lecture 5: Neural Network (2) | 2023.01.11 |
| [EECS 498-007 / 598-005] Lecture 3: Linear Classifiers (2) | 2023.01.06 |



