- 본 게시글은 Justin Johnson 교수님의 Deep Learning for Computer Vision, University of Michigan 정리글입니다.
- 개인적인 생각이 서술되어 있습니다. 잘못된 내용이 존재할 확률이 존재하기에 주의 바랍니다.
- 잘못된 내용, 오타는 지적해 주시면 감사하겠습니다.
강의링크:
https://www.youtube.com/watch?v=dB-u77Y5a6A&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=6
강의자료:
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture06.pdf
이전 강의에서 Gradient를 계산하는 방법들을 살펴보았습니다. 하지만 이를 계산하는 것은 문제가 있습니다.
- 매우 지루하며, 많은 연산이 요구됩니다.
- Loss를 바꾸고 싶을때 모듈만 바꾸면 되는 것이 아니라, 처음부터 다시 진행해야 합니다.
- 복잡한 모델에서는 적합하지 않습니다.
그럼 좋은 방법은 뭘까요?
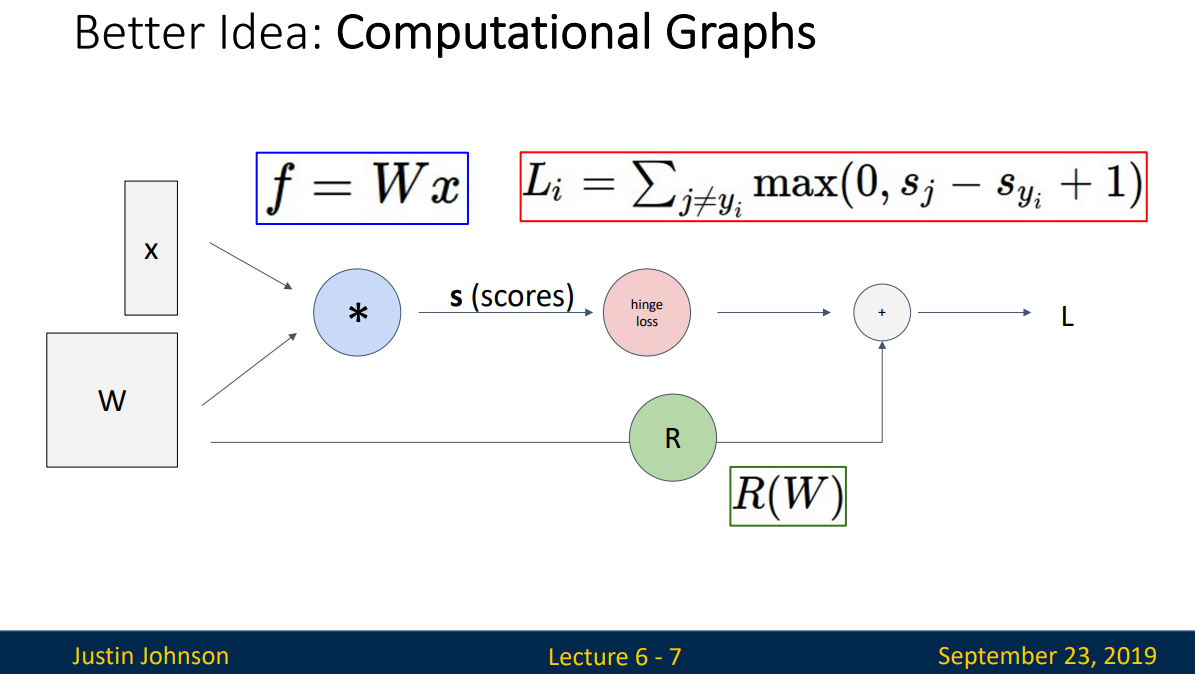
Computational Graphs는 연산을 graph로 표현한 것입니다. f=Wx, loss function, Regularization term이 모두 graph로 표현된 것을 확인할 수 있습니다. Linear classifier를 표현할 때는 굳이 graph가 필요하지 않다고 생각하실 수 있겠지만, neural net에서는 layer가 커지는 등 모델이 복잡해질수록 이는 중요해집니다.
아래의 그림은 Graph로 표현한 AlexNet입니다.

1. Backpropagation: Simple Example

Forward pass는 output을 계산해나가는 과정입니다. 예제에서는 q= x+y, f=qz를 순차적으로 계산하였습니다.
반면 Backward pass는 변수 x, y, z에 관한 미분값을 계산해나가는 과정입니다.
그럼 df / dx, df / dy는 어떻게 계산할까요?
f는 q, z와는 직접적으로 연결되어있지만, x,y는 그렇지 않습니다. 이때 Chain Rule을 사용합니다.
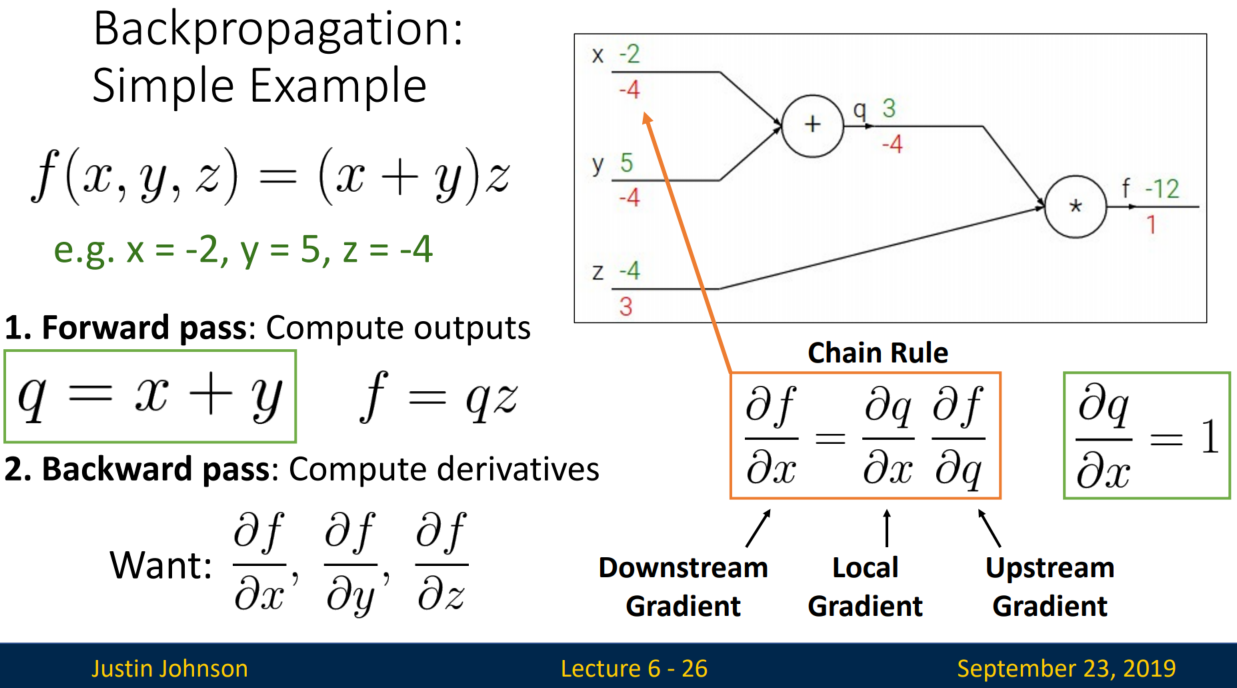
Chain Rule은 뒤에서부터 계산합니다. 예를 들어, df / dq = z (-4), dq / dx = 1이므로 df / dx = -4가 됩니다.
Downstream, Local, Upstream Gradient에 관한 설명은 다음과 같습니다.

* Downstream Gradient: 노드의 입력 변수에 관한 Gradient
* Local Gradient: 지역적으로 연산되는 Gradient
* Upstream Gradient: 노드의 출력 변수에 관한 Gradient
다른 예제를 추가적으로 살펴보겠습니다.
로지스틱 회귀 함수의 Forward pass는 다음과 같습니다.

그럼 Backward pass를 살펴볼까요?
1. df / df = 1이기에, 첫 번째 Upstream Gradient는 1입니다. Downstream Gradient는 1/x를 x에 대해 편미분한 Local Gradient를 계산한 다음 Upstream Gradient, 1과 곱하여 계산합니다.
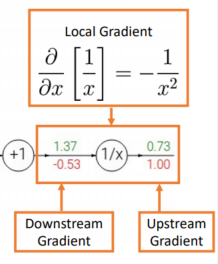
2. 계산된 Downstream Gradient를 다음 단계의 Upstream Gradient로 사용하여, 같은 알고리즘으로 계산을 반복합니다.
3. 동일한 알고리즘을 끝까지 반복하면, 모든 변수에 대한 Downstream Gradient를 다음과 같이 계산할 수 있습니다.

여기서 한 가지 의문이 듭니다. 바로, 연산량이 너무 많다는 점입니다. 다행히 이 문제를 해결할 수 있는 방법이 있습니다. 'Sigmoid 함수'를 local gradient로 사용하는 것입니다.

sigmoid 함수는, 미분값에 원래 함수가 들어있는 성질이 있습니다.
즉 복잡한 연산을 진행하지 않고도 손쉽게 미분값을 연산할 수 있다는 뜻입니다!

위의 예제를 Sigmoid 함수를 통해 계산하면 아래와 같습니다.

순차적으로 중간 과정을 지행할 필요 없이 아래처럼 손쉽게 계산할 수 있습니다.
Downstream = Local x Upstream
= {(1-0.73) x 0.73} x 1 = 0.2
이는 Local 과정을 (1-sigmoid) x sigmoid로 대체하였기에 가능해졌습니다.
* Local의 범위는 분기되는 지점(input 방향이 2개 이상)없이, 단일 방향으로 이동하는 범위만 가능할 것 같습니다. 단일 방향은 함수와 다른 함수를 결합하여 새로운 함수라고 인식하면 되지만, 분기되는 지점은 그것이 불가능하기 때문입니다.
2. Patterns in Gradient Flow
Backpropagation을 계산할 때, 연산자에 따른 패턴이 있습니다. 이를 알면 연산과 코딩에 도움을 받을 수 있기에 살펴보겠습니다.

- add gate: gradient distributor. +의 Local Gradient는 1이기에 Downstream = 1 x Upstream이 됩니다.
- copy gate: gradient adder.
- mul gate: swap multiplier. f = xy가 있다고 가정해보겠습니다. 이때 x에 대해 편미분하면 y가 남기에 Local Gradient는 y가 됩니다. 이러한 성질로 swap multiplier로 불리게 된 듯 합니다.
- max gate: gradient router.
이 성질을 응용하면, 수학적 연산 없이 코딩을 할 수 있습니다.
먼저 자신에 관한 편미분, Upstream = 1로 시작합니다.

다음으로, Sigmoid 함수의 성질을 이용합니다.

s3가 끝났으니, w2와 s2의 Backpropagation을 진행할 차례입니다.
근데 s3 = s2 + w2의 성질이 보이시나요? add gate에 따르면 다음이 성립합니다.
s3의 미분값 = s2의 미분값 = w2의 미분값

s2또한 add gate로 이루어져있습니다. 따라서,
s2의 미분값 = s0의 미분값 = s1의 미분값

s1은 w1 X x1으로 mul gate이니, swap multiplier 성질을 적용합니다.
w1의 미분값 = s1의 미분값 X x1
x1의 미분값 = s1의 미분값 X w1
최종적으로 다음의 값으로 계산됩니다. 각 진행 단계를따라 검산해 보세요!

지금까지 Scalar로만 Backpropagation을 진행했습니다. 그러나, Lecture 3부터 살펴봤듯이 대부분은 Vector로 이루어져있습니다. 그럼 Vector Backpropagation을 살펴보겠습니다.
3. Backprop with Vectors

- Regular derivative, 1x1 (Scalar): x에 미세한 변화 생기면, y는 얼만큼 변화할까요?
- Derivative is Gradient, Nx1 (Vector): x의 각 요소에 미세한 변화 생기면, y는 얼만큼 변화할까요?
- Derivative is Jacobian, NxM (Matrix): x의 각 요소에 미세한 변화 생기면, y의 각 요소는 얼만큼 변화할까요?
* Jacobian을 공부하고 싶은 분들은 아래의 블로그를 참고하면 큰 도움을 받으실 수 있습니다.
자코비안(Jacobian) 행렬의 기하학적 의미 - 공돌이의 수학정리노트
angeloyeo.github.io
아래 그림을 통해 자세히 살펴보겠습니다.

x의 차원은 x X 1(Vector), y의 차원은 y X 1(Vector), z의 차원은 z X 1(Vector)입니다.
하지만 loss는 여전히 Scalar입니다.!!
1. Upstream Gradient
dL / dz는 loss(Scalar)를 z(Vector)로 편미분한 형태로 z X 1 vector가 됩니다. → Derivative is Gradient
Vector z의 각 요소들이 loss에 얼만큼 영향을 미치는지를 나타냅니다.
2. Local Gradient
dz / dx는 x(Vector)와 z(Vector)의 행렬 곱이기에 x X z matrix가 됩니다. 마찬가지로 dz / dy는 y X z matrix가 됩니다.
3. Downstream Gradient
Downstream = Local x Upstream이기에, 이를 활용해보겠습니다.
x = matrix(x X z) X vector(z X 1) = vector(x X 1)
y = matrix(y X z) X vector(z X 1) = vector(y X 1)
Backpropagation에서 Sigmoid 대신 ReLU 함수를 사용한 과정은 다음과 같습니다.

ReLU 함수는 음수는 0으로 만들기에 단위행렬(I)에서 해당 행은 0으로 설정합니다. 그럼 음수가 입력된 행은 값이 안 나오겠죠? 다만 문제가 있습니다.
해당 위치를 제외(off-diagonal)하고는 모두 0 이기에, 행렬이 커질수록 비효율적이 됩니다. 이 문제를 해결하고자 다음과 같이 표현합니다.

다음으로 Matrix Multiplication을 살펴보겠습니다.

Forward pass는 x X w = y (크기: NxDxDxM → NxM)로 진행됩니다. 다만 Matrix 연산을 수행하기위해서는 행렬곱에 관한 지식이 있어야 합니다. 예시로 y의 첫 행, 첫 열 인자 (-1)를 계산해보겠습니다.
y_11 = x_11 X w_11 + x_12 X w_21 + x_13 + w_31
-1 = 2 X 3 + 1 X 2 + (-3) X 3
다음으로 Backpropagation 진행을 살펴보겠습니다.

Downstream Gradient = Local Gradient X Upstream Gradient
Loss는 Scalar 값으로 나온다고 하였습니다. 맞습니다.
하지만 dL / dy는 Scalar 값을 N x M matrix로 미분한 값이기에 matrix 형태가 됩니다. 그리고 이는 Upstream Gradient가 됩니다. 다음으로 Local Gradient를 구해야합니다.
그런데, Matrix가 커짐에 따라 Local Gradient를 순차적으로 일일히 계산하는 것은 힘듭니다. 따라서 각 요소별로 확인해보겠습니다.
y_11 = x_11 X w_11 + x_12 X w_21 + x_13 + w_31
→ dy_11 / dx_11 = w_11 이 됩니다.
동일한 원리로 dy_12 / dx_11 = w_12, dy_13 / dx_11 = w_13, dy_14 / dx_11 = w_14가 됩니다.
다음으로 y_21 = x_21 X w_11 + x_22 X w_21 + x_23 + w_31
→ dy_21 / dx_11 = 0 입니다. dx_11 인자가 없기 때문이죠.
계산을 순차적으로 살펴보겠습니다.



'공부 정리 > Machine learning & Deep learning' 카테고리의 다른 글
| [EECS 498-007 / 598-005] Lecture 8: CNN Architectures (0) | 2023.01.26 |
|---|---|
| [EECS 498-007 / 598-005] Lecture 7: Convolutional Networks (0) | 2023.01.24 |
| [EECS 498-007 / 598-005] Lecture 5: Neural Network (2) | 2023.01.11 |
| [EECS 498-007 / 598-005] Lecture 4: Optimization (0) | 2023.01.08 |
| [EECS 498-007 / 598-005] Lecture 3: Linear Classifiers (2) | 2023.01.06 |



