- 본 게시글은 Justin Johnson 교수님의 Deep Learning for Computer Vision, University of Michigan 정리글입니다.
- 개인적인 생각이 서술되어 있습니다. 잘못된 내용이 존재할 확률이 존재하기에 주의 바랍니다.
- 잘못된 내용, 오타는 지적해 주시면 감사하겠습니다.
강의링크:
https://www.youtube.com/watch?v=g6InpdhUblE&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=5&t=1483s
강의자료:
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture05.pdf
기타 자료: 고려대학교 김성범 교수님(DMQA) 강의자료 및 강의영상
https://www.youtube.com/watch?v=YIgLpsJ-1J4
Previous
Lecture 3&4에서는 다음 3가지를 배웠습니다.
1. Linear Models for image classification
2. Loss Functions to express preferences
*small means good
3. Various Optimizer including SGD

Linear Classifers(선형 분류기)는 막 좋지는 않습니다.
왜 그럴까요? 비선형 문제가 훨씬 더 많기 때문입니다.
이 문제를 해결하는 방법은 간단합니다. 비선형 문제를 고차원으로 이동하여, 선형인 상황을 만들면 됩니다. 대표적으로 비선형 SVM 기법이 있습니다.

강의에서는 극좌표계를 예시로 Feature transform을 진행하였습니다. 이를 통해 Original space에서는 비선형이었던 분류 문제가, Feature space에서는 선형으로 분류 가능하게 되었습니다.
+ 극좌표계를 활용하면 복소수 등을 표현할 수 있기에 알아두면 유용한 기법이라고 생각합니다.
* 극좌표계: 평면 위의 위치를 각도와 거리를 써서 나타내는 2차원 좌표계(위키백과 참조)
그럼 이미지의 Feature는 어떻게 추출할까요? 다음의 기법을 살펴봅니다.
- Color Hisogram
- Histogram of Oriented Gradients (HoG)
- Bag of Words (BoW)
Color Hisogram은 질감, 공간 정보를 고려하지 않고 색상만을 고려한 Histogram입니다. 빈도를 통해 이미지의 색 분포, 주로 어떤 색을 띠는지 확인 가능합니다.

HoG는 각 pixel의 edge 방향 / 강도만을 남겨두고, 이를 활용하여 이미지를 분석합니다. 파란 부분처럼 edge 가 뚜렷하다면 선명하게, 노란 부분처럼 edge가 뚜렷하지 않다면 거의 보이지 않도록 추출합니다.

앞의 두 기법은 Feature를 어떻게 추출할 것인가에 관한 방법입니다. 그에 반해 BoW는 Data-Driven 방법입니다. BoW는 NLP(자연어 처리)에서 주로 사용되는 기법으로, 순서를 고려하지 않고 빈도에만 집중하는 방법입니다.

- Step 1에서는 patch를 random하게 추출한 뒤, patch를 clustering 하여 codebook을 만듭니다. 그림 조각들을 만들었다고 생각하면 될 듯합니다.
- Step 2에서는 clustering 된 patch의 빈도를 산출합니다.
*NLP에서의 단어를 이미지에서는 patch로 만든 뒤, 진행하였다고 이해했습니다.
Feature Extraction은 좋은 기법입니다. 하지만 사람이 Feature를 설정하여야 하기에 성능 차이가 크고 복잡합니다. 하지만 Nerual Networks는 컴퓨터가 스스로 진행합니다! 그럼 지금부터 Neural Networks를 알아보겠습니다.
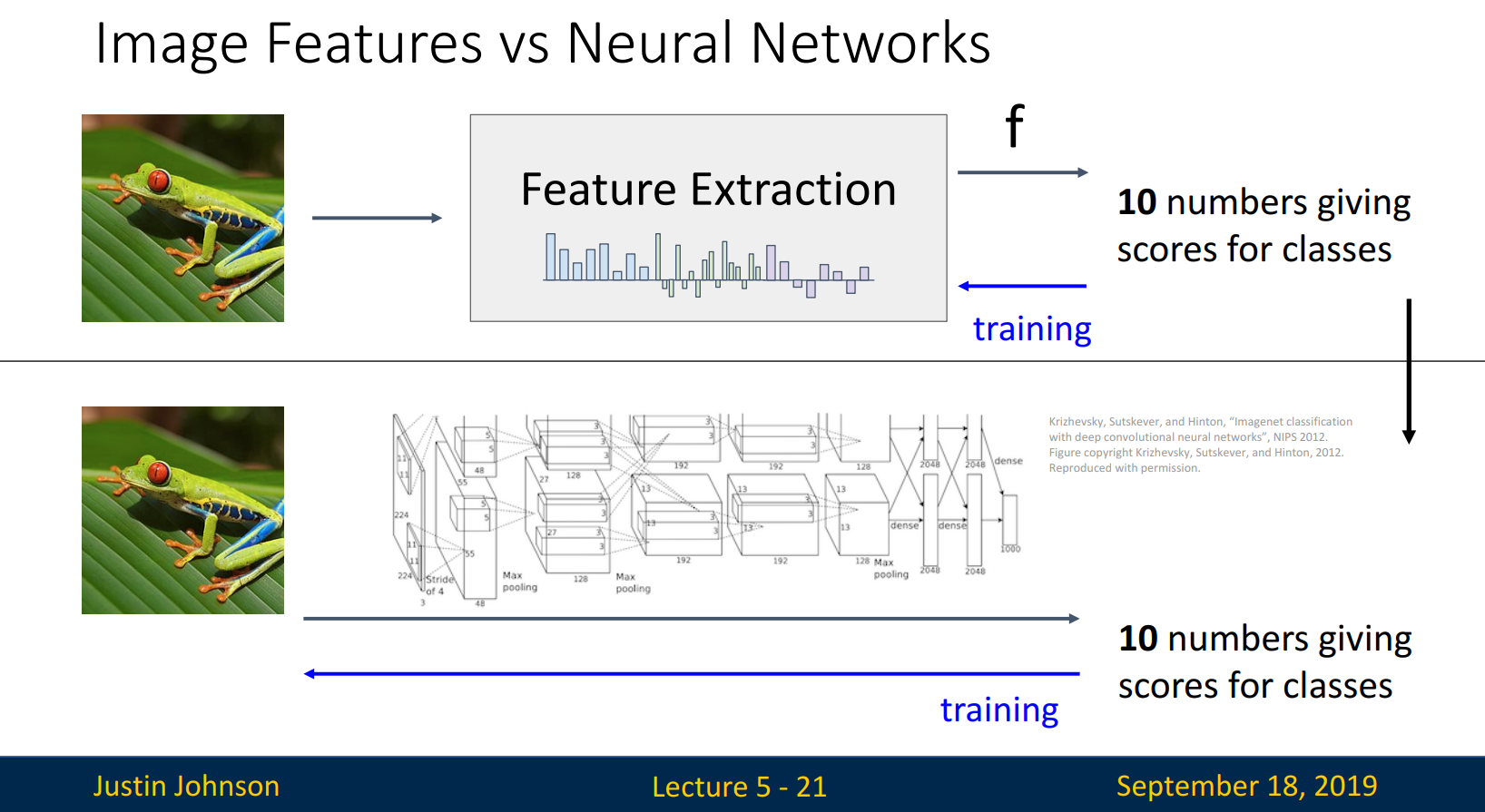
5.1. Neural Networks

이전 시간에 f = Wx를 배웠습니다. Neural Networks에서는 f=Wx를 layer(층)를 쌓습니다. 만들어진 f로 다시 layer를 쌓고, 또 이를 반복합니다.
*각 layer에도 학습 가능한 bias를 추가합니다.
아래의 그림은 이해에 큰 도움이 됩니다.

Y가 연속형 / 범주형인지에 따라 선형회귀 모델 / 로지스틱 회귀모델로 기본적인 표현이 가능합니다. 로지스틱 회귀모델의 지수를 보시면 선형회귀 식이 포함되어 있음을 확인할 수 있습니다. 이렇게 만들어진 로지스틱 회귀식은 뉴럴네트워크의 지수로 들어가게 됩니다. 만들어진 뉴럴네트워크는 아래 그림처럼 표현 가능합니다.
*선형회귀 모델: Y가 연속형일 때, 입력변수(X)의 선형결합으로 출력변수(Y)를 표현
*로지스틱 회귀모델: Y 가 범주형일 때, 입력변수(X)의 비선형결합(로지스틱 함수 형태)으로 출력변수(Y)를 표현
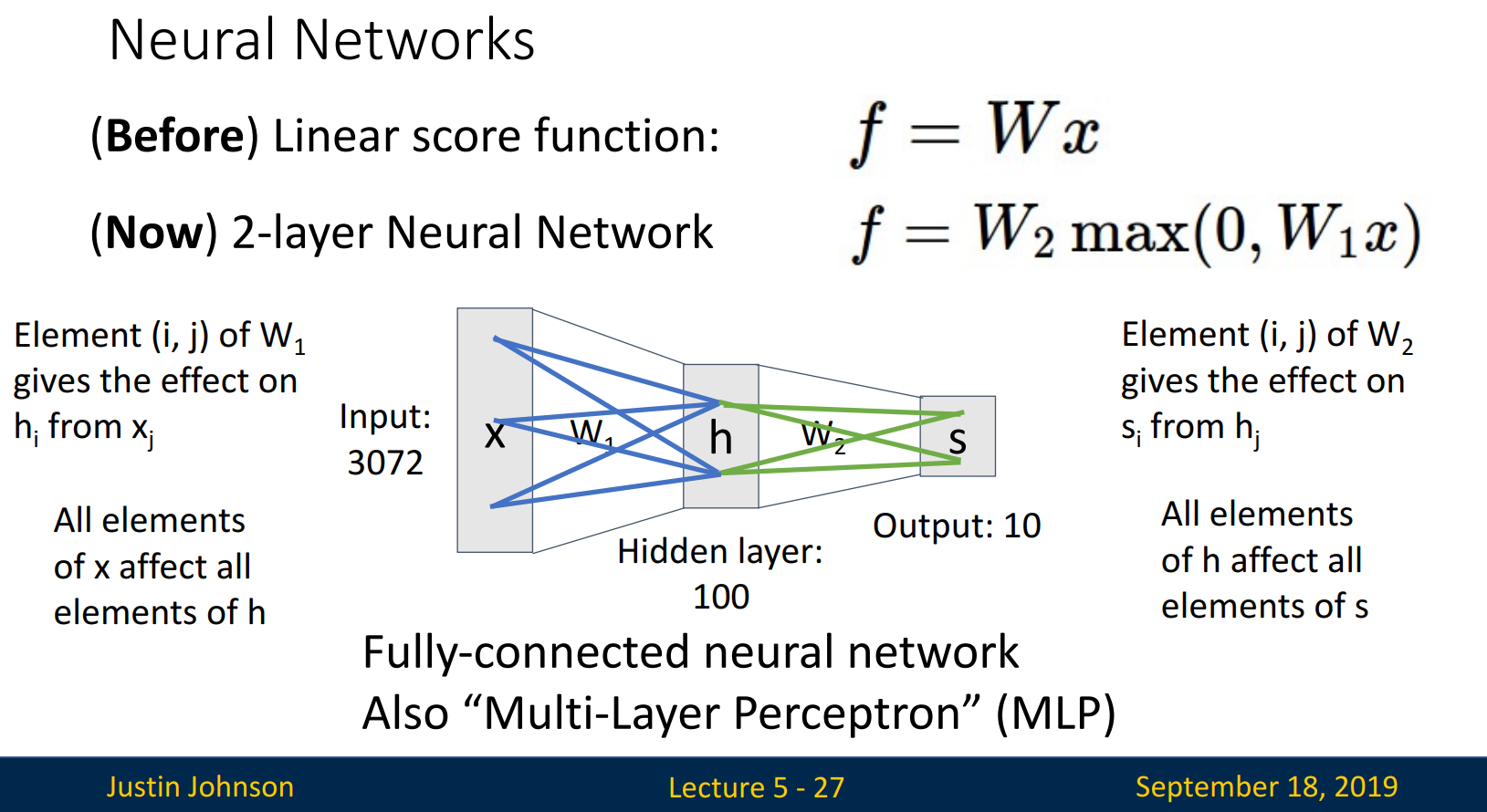
W1의 (i, j)는 x_j - h_i연결에 영향을, W2의 (i, j)는 h_j - s_i연결에 영향을 줍니다. 이때 i와 j는 해당되는 모든 elements입니다. 따라서 Fully-connected neural network, Multi-Layer Perceptron (MLP)라고도 불립니다.
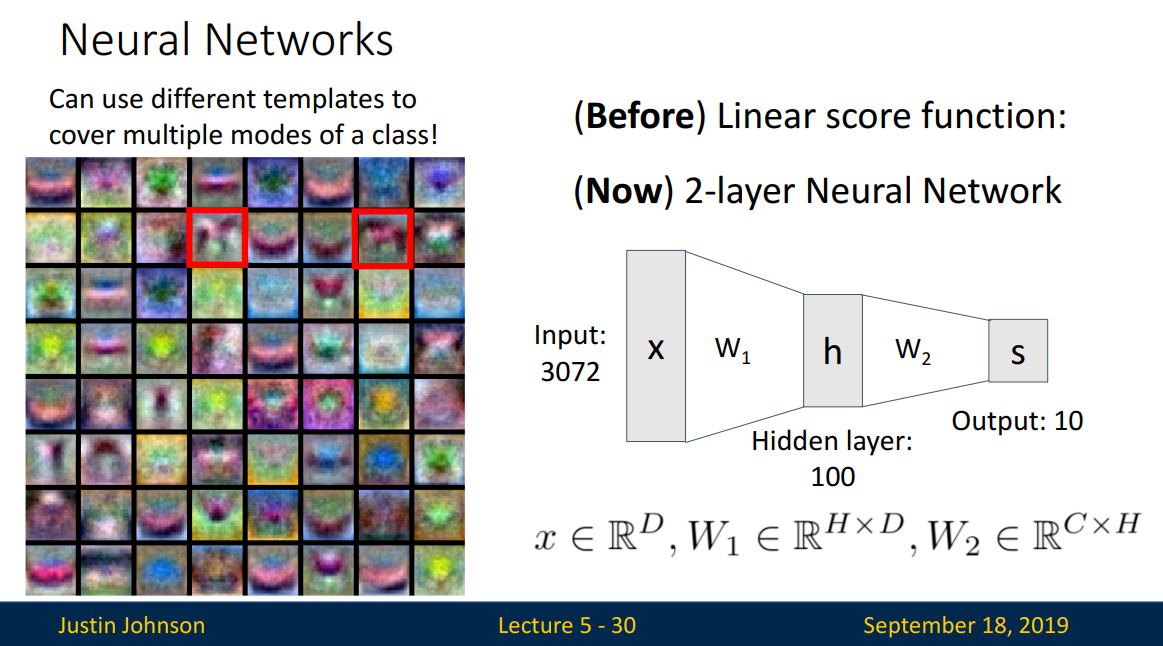
CIFAR-10 데이터의 카테고리당 여러 개의 template를 생성했습니다. 첫 번째 layer에서는 weight의 크기만큼 template을 만들어내고, 두 번째 layer에서는 첫 번째 layer에서 만들어진 template을 recombine 하여 template을 생성합니다. 특징은 다음과 같습니다.
- 카테고리의 여러 표현 방법을 만들 수 있습니다. 아래의 horse는 서로 다른 방향(바라보는 방향)으로 만들어졌습니다.
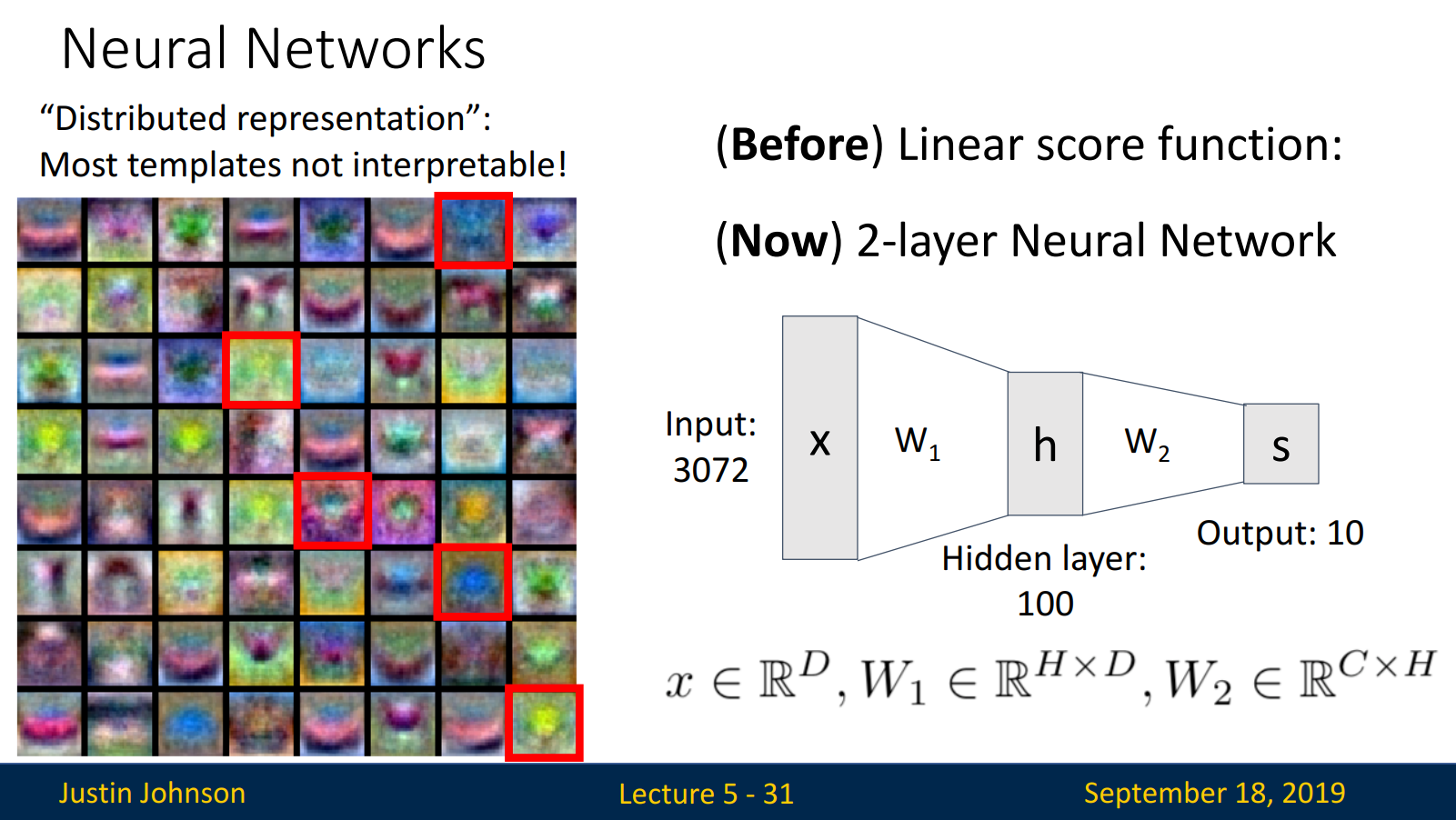
- Distributed representation: 대부분의 template은 해석 불가능합니다. 딥러닝의 단점이랄까요..
Deep Neural Networks의 구조는 다음과 같습니다. 일반적으로 layer의 개수는 #(number) of weight로 표현됩니다.
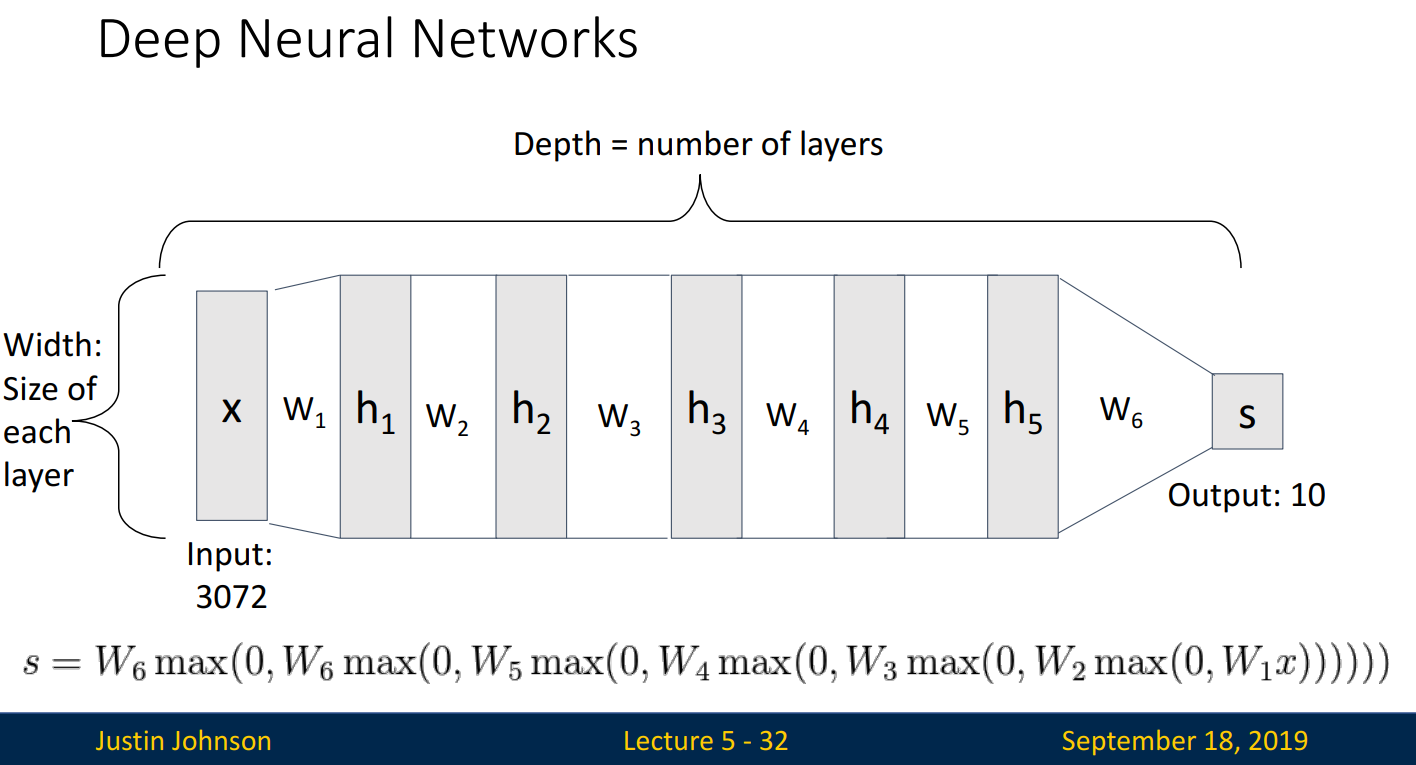
5.2. Activation Functions
Neural Networks에서는 입력 값들을 다음 layer로 이동할 때, 비선형 함수인 활성화 함수에 먼저 통과시킵니다.
입력 값 → Activation Functions(활성화 함수) → Layer

Q. What happens if we build a neural network with no activation function?
A. We end up with a linear classifier!
그럼 선형 분류기의 문제가 무엇일까요?
선형 분류기는 Neural Networks의 장점을 살리지 못합니다.
선형 함수를 사용하면 위 그림에 나와있듯이, W3 = W2 x W1 이 됩니다. 즉 Layer가 추가되는 효과 없이, 그저 상수를 곱한 효과만을 보게 됩니다.
반면, 비선형 함수를 사용하게 되면 선형 함수 2개(ReLU 기준, y=0 & y=x)를 사용하는 효과가 있어, Layer가 추가될수록 (두 선형 함수) x (두 선형 함수) x... 의 효과를 볼 수 있습니다.
이를 요약하면 (활성화 함수로) 선형 함수를 사용하면 은닉층 1개 효과만을, 비선형 함수를 사용하면 은닉층 여러 개 효과를 볼 수 있습니다.
*활성화 함수가 없는 model을 Deep linear network라고 부릅니다. 그래도 이는 최적화 관점에서는 연구할만하다고 합니다.
활성화 함수는 아래의 그림처럼 여러 종류가 있습니다. 그중 ReLU가 대다수의 문제에서 좋다고 합니다.

Space Warping
비선형 함수의 또 다른 장점은 Space Warping입니다. 선형 분류기 2개를 새로운 축으로 설정한 뒤 +,-의 조합으로 A, B, C, D를 만들었습니다.
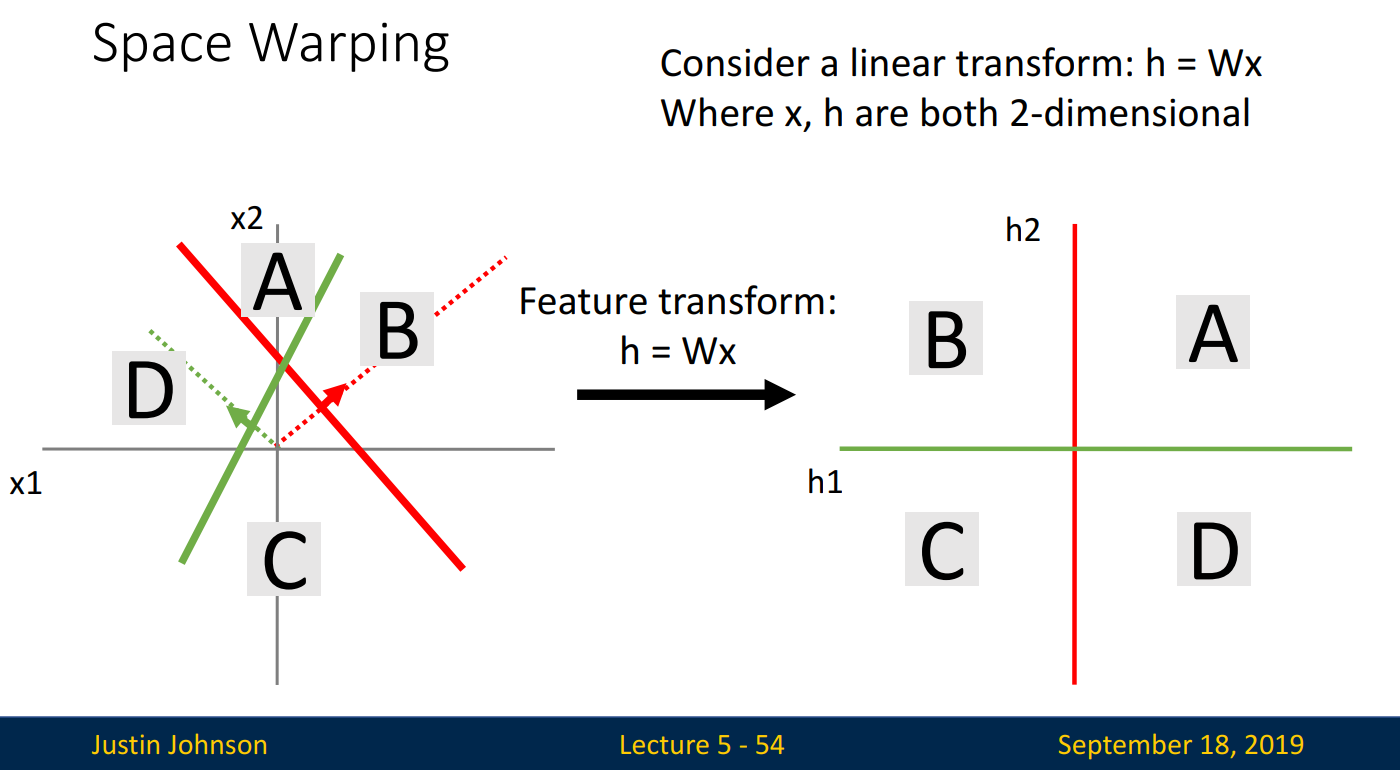
하지만 선형 분류기로는, 두 집단을 직선으로 완벽히 분류할 수 없을 수도 있습니다. 선형 분류기를 기준으로 분류한 아래의 오른쪽 그림에서는, 어떤 직선으로도 완벽히 분류할 수 없습니다.
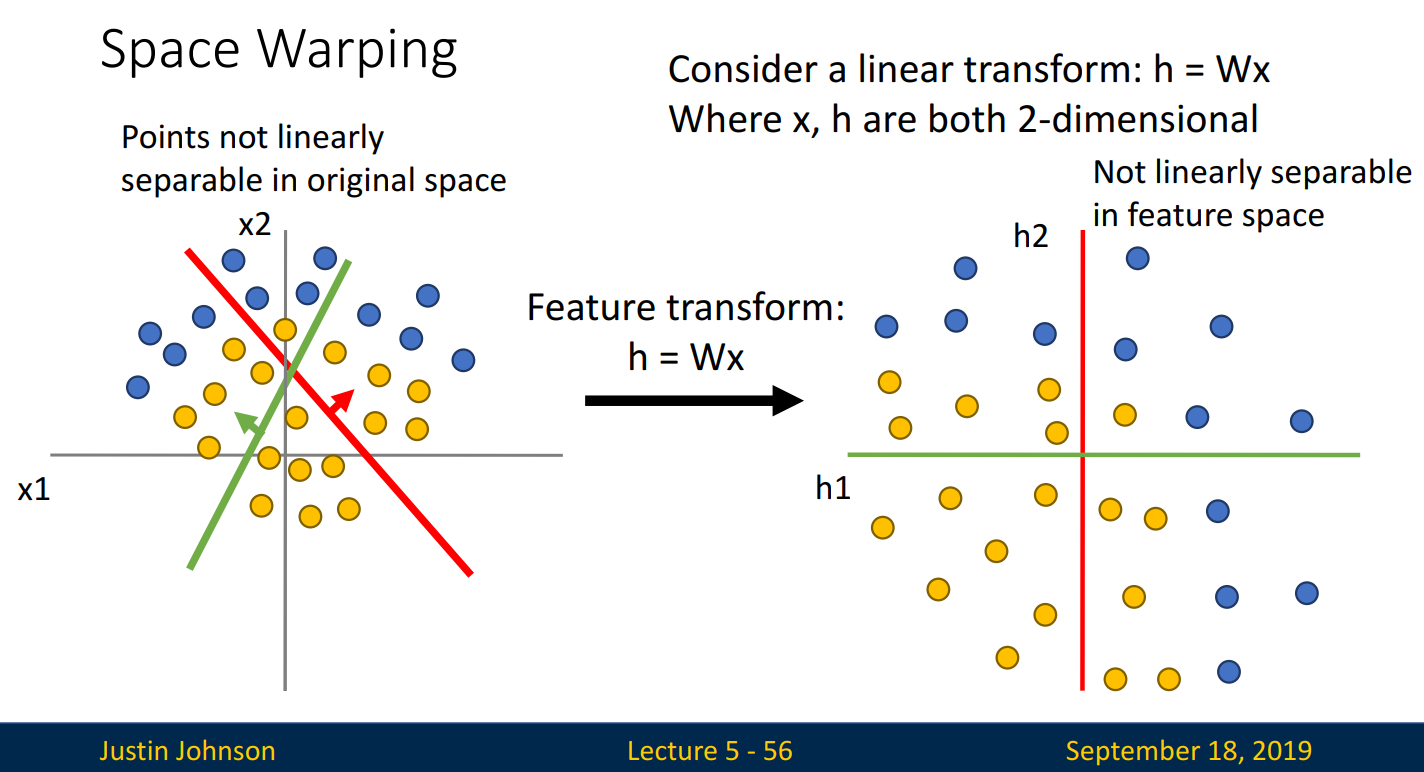
그럼 대표적인 활성화 함수, ReLU를 사용하면 어떻게 될까요?
ReLU를 사용하면 x < 0인 값은 → 0, x > 0인 값은 → x(원래 값)으로 매핑됩니다.
- A: 초록선 기준 +, 빨간 선 기준 + 이기에 원래 값으로 매핑됩니다.
- B: 초록선 기준 -, 빨간 선 기준 + 이기에 초록선 값=0, 빨간선 값=x로 매핑됩니다. 빨간선 축으로 사영된다고 생각하면 됩니다. (-2, 3)인 값이 (0,3)으로 바뀌는 것처럼 말입니다.
- C: 초록선 기준 -, 빨간선 기준 - 이기에 초록선 값=0, 빨간선 값=0, 즉 원점(0,0)으로 매핑됩니다.
- D: 초록선 기준 +, 빨간선 기준 - 이기에 초록선 값=x, 빨간선 값=0으로 매핑됩니다.
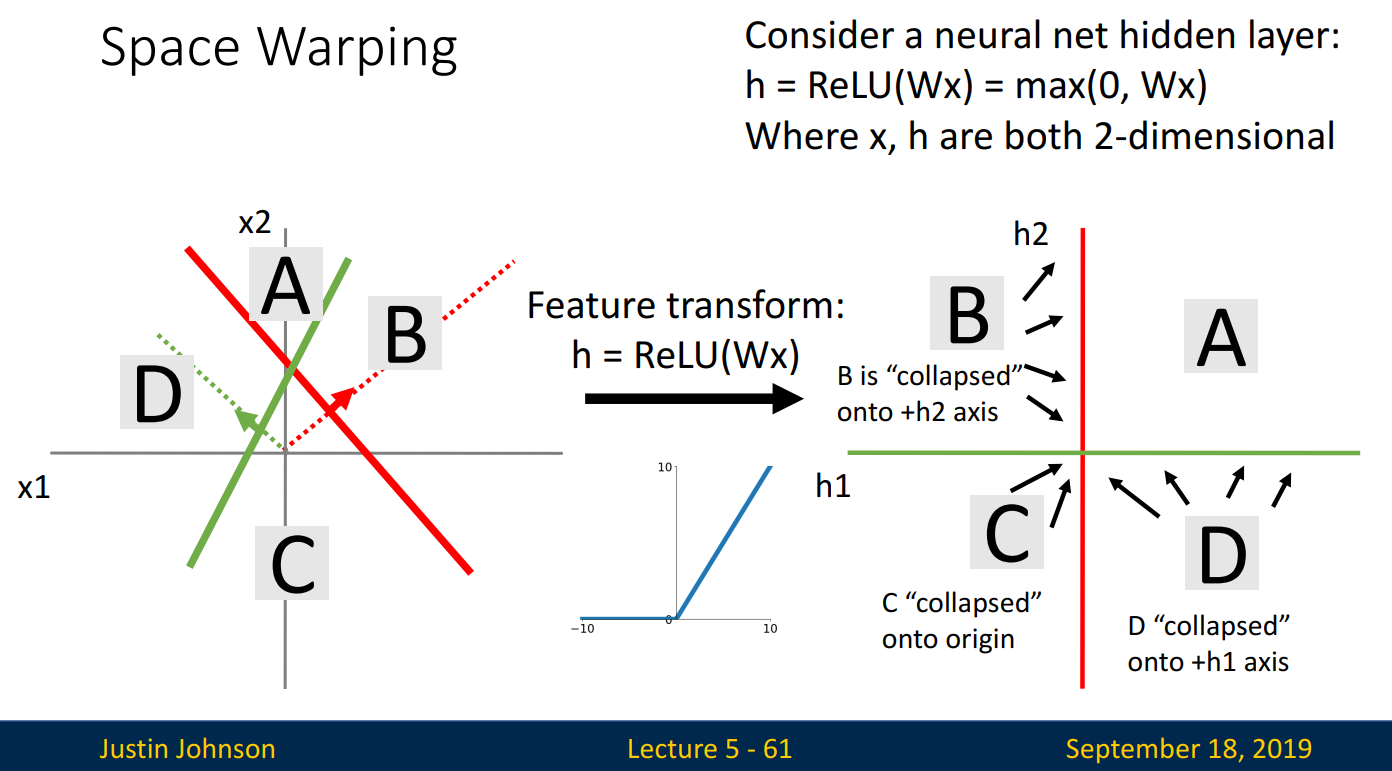
활성화 함수를 통해 새로운 축에 사영된 점들은, 직선으로 완벽히 분류할 수 있게 됩니다.
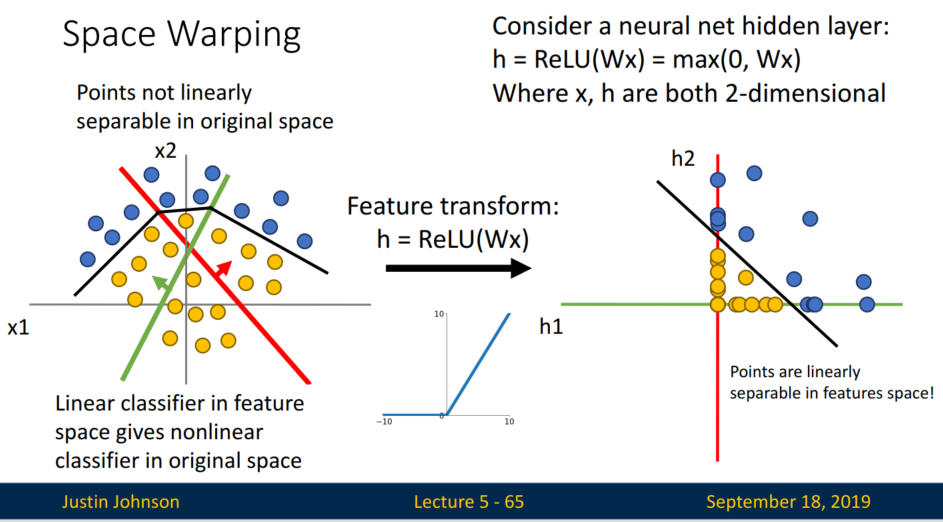
만약 은닉층(hidden layer)이 깊어진다면 어떻게 될까요? Original space에서 선이 증가하며, (Feature transform을 거친) Feature space에서는 훨씬 복잡하게 선형 분리되게 됩니다. 이를 다시 Original space에서 보게 된다면 복잡한 비선형 결정 경계(Decision boundary)로 나타나게 됩니다.
*강의에서 space folding을 언급하였는데 layer별로 transformation이 단계대로 진행되니, 이를 folding 하였다고 표현한 것 같습니다. 한 번에 진행하는 게 아니라 접고, 접고, 접고... 이런 느낌인 듯합니다.
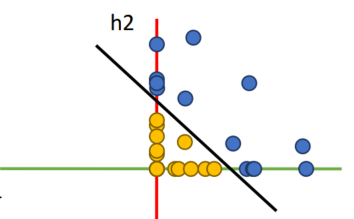
Feature space상의 선형이,
↓
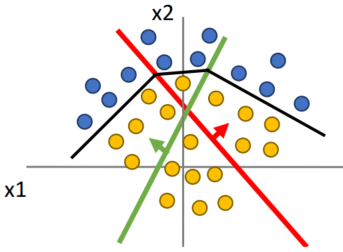
Original space상의 비선형 결정 경계가 됩니다.
복잡한 은닉층은 overfitting 문제를 일으킵니다. 그럼 이를 방지하기 위해 은닉층을 줄이는 게 해답일까요?
아닙니다. 은닉층을 줄이기보다 정규화를 활용해야 합니다.
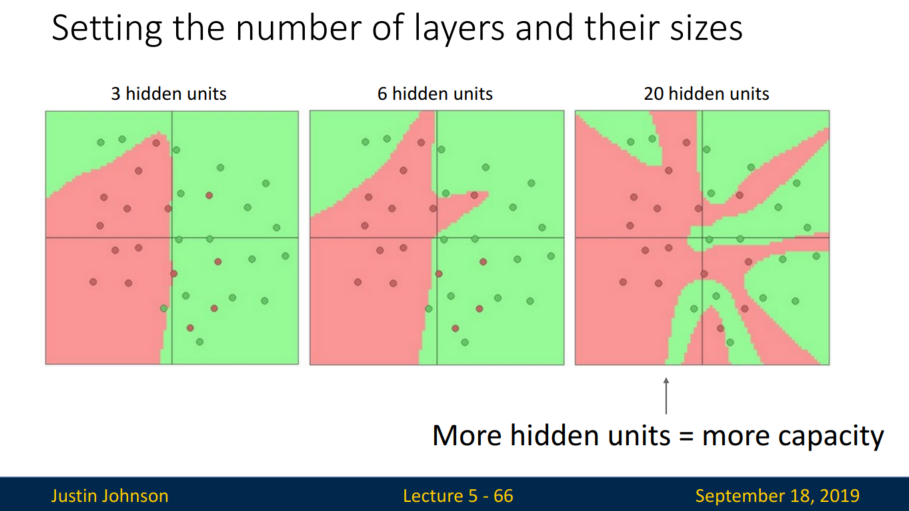
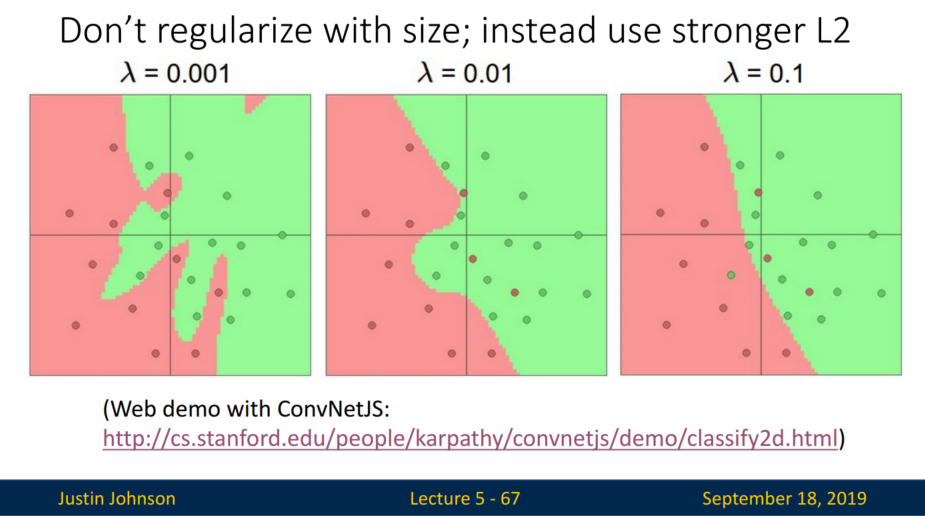
L2 norm을 활용하여 정규화를 시킬 수 있습니다. 람다 값이 커질수록 점들을 완벽히 분류할 수는 없겠지만, 선형에 가까워집니다.
Universal Approximation
Universal Approximation은 은닉층 1개 & 비선형 활성화 함수로 이루어진 Neural network는, 어떠한 형태의 연속함수로든 근사하여 표현이 가능함을 말합니다.
예제로 two-layer ReLU network를 다루어봅니다.

은닉층의 hidden unit(h1, h2, h3)을 활성화 함수(ReLU) 형태로 나타낼 수 있고, Output, y는 이들의 선형 결합 형태로 표현 가능합니다. 이는 y가 shifted, scaled ReLU의 합으로 표현 가능함을 의미합니다.
shifted, scaled ReLU를 통해 어떠한 형태의 함수에 대한 근사를 표현할 수 있습니다. 이를 'bump function'고 말합니다.
그림을 통해 자세히 살펴보겠습니다.
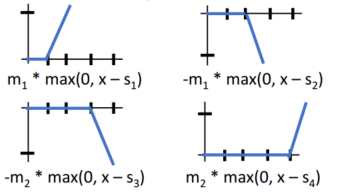
shifted, scaled 된 ReLU, 4개가 있습니다.
이는 h1, h2, h3, h4가 됩니다. 그리고
각 hidden unit(h1, h2, h3, h4)을 선형결합하면,
↓
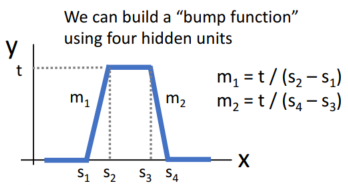
h1, h2, h3, h4를 선형결합한 bump function이 만들어집니다.
이를 활용하면 어떠한 연속 함수로든 근사 가능하고,
이는 two-layer만으로 universal(보편적인) 근사가 가능함을 의미합니다.
↓
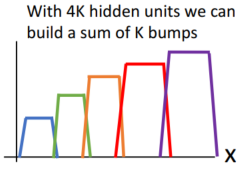
two-layer로 만들어진 bump를 k번 합하면 이와 같습니다.
↓
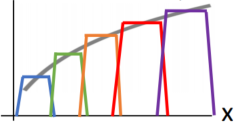
점점 함수에 근사하게 되죠?
Universal approximation tells us
- Neural nets can represent any function(모든 함수를 나타낼 수 있습니다)
Universal approximation DOES NOT tell us
- Whether we can actually learn any function with SGD
- How much data we need to learn a function
5.3. Convex Functions
아래의 식이 성립할 때, Convex Function(볼록 함수)이라고 말할 수 있습니다.
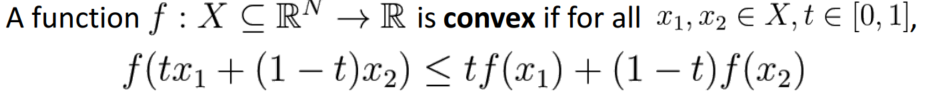
Convex function인 f(x) = x**2를 살펴보겠습니다.
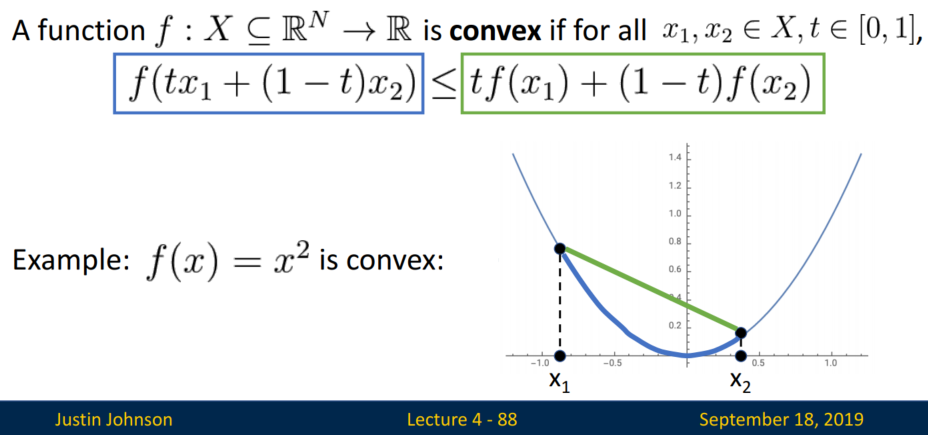
(x1, x2)에서 파란색으로 표시된 부분은 항상 초록색으로 표시된 부분보다 작습니다.
다차원일 때는 아래의 bowl처럼 움푹 파인 모양일 것임을 상상할 수 있습니다.
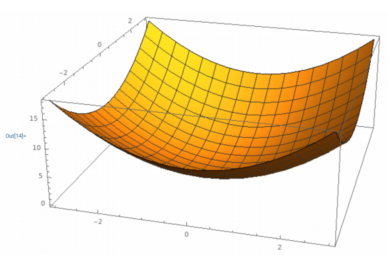
Convex function은 왜 중요할까요? 최적화(optimization)가 쉽습니다.
전역 최솟값(global minimum)으로 이동함을 이론적으로 보장할 수 있기에, 즉 Convex function이면 정답을 구할 수 있습니다. 어느 곳에서나 기울기가 감소하는 방향으로 이동한다면 전역 최솟값에 도달하기 때문입니다.
앞 강의에서 'Linear classifier를 왜 이렇게 자세히 배우지?'는 의문이 들었던 분들이 계실 겁니다. 이는 convex function을 위한 배움이었습니다. Linear classifer는 convex function이기에 전역 최소값에 도달할 수 있다는 이론적 보장이 있기 때문입니다.

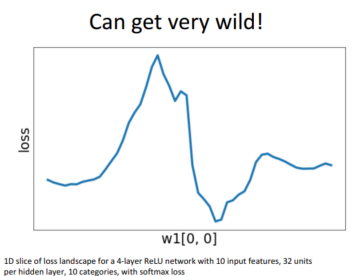
Neural network도 전역 최소값에 도달할 수 있다는 이론적 보장이 있을까요?
아쉽게도 없습니다. 그렇기에 nonconvex optimization이 필요합니다. 이런 이유로 혹자는 Linear classifier를 좋아하기도 하죠. 그럼에도 Neural network는 경험적으로 꽤나 잘 작동한다고 합니다 : )
태연자약(泰然自若):
마음에 어떠한 충동을 받아도 움직임이 없이 천연스러움
내일은 조금 더, 태연자약한 하루가 되기를 소망합니다.
'공부 정리 > Machine learning & Deep learning' 카테고리의 다른 글
| [EECS 498-007 / 598-005] Lecture 8: CNN Architectures (0) | 2023.01.26 |
|---|---|
| [EECS 498-007 / 598-005] Lecture 7: Convolutional Networks (0) | 2023.01.24 |
| [EECS 498-007 / 598-005] Lecture 6: Backpropagation (0) | 2023.01.17 |
| [EECS 498-007 / 598-005] Lecture 4: Optimization (0) | 2023.01.08 |
| [EECS 498-007 / 598-005] Lecture 3: Linear Classifiers (2) | 2023.01.06 |



