- 본 게시글은 Justin Johnson 교수님의 Deep Learning for Computer Vision, University of Michigan 정리글입니다.
- 개인적인 생각이 서술되어 있습니다. 잘못된 내용이 존재할 확률이 존재하기에 주의 바랍니다.
- 잘못된 내용, 오타는 지적해 주시면 감사하겠습니다.
강의링크:
https://www.youtube.com/watch?v=igP03FXZqgo&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=20
강의자료:
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture20.pdf

지난 게시물에서는 Autorgressive와 VAE에 대해 살펴보았습니다. 이번 시간에는 이전 시간에 못다 한 VAE 뒷부분과, GANs을 알아보겠습니다.
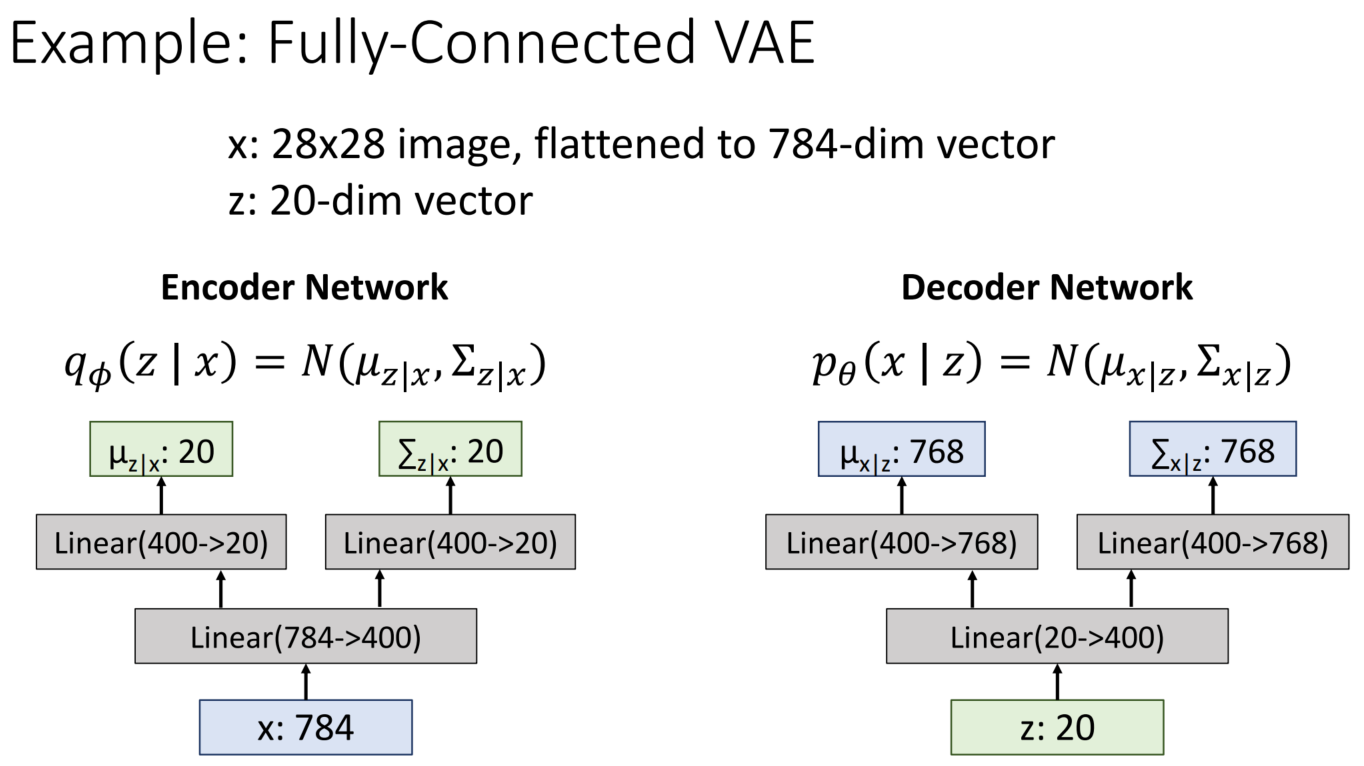
Fully-Connected VAE로 예시를 들어보면 위의 그림과 같이 구성할 수 있습니다.
*768은 오타입니다. 784가 맞습니다.
VAE: Training
총 6단계로 구성된 VAE의 순서를 살펴보겠습니다.

1. Run input data through encoder to get a distribution over latent codes
Encoder에 input 데이터를 입력 → input에 관한 latent(z)의 분포를 얻습니다.
2. Encoder output should match the prior p(z)!
Encoder의 output은 p(z)와 최대한 비슷해야 합니다. Encoder의 output: q_phi(z|x)와 p(z)의 차이를 D_KL을 통해 표현, 이 값이 작아져야만 전체 식이 최대화가 되기에 차이를 줄여나가는 방향으로 학습합니다.

3. Sample code z from encoder output
앞서 구한 분포로부터 각 z를 samping 하여 code z를 구합니다.
4. Run sampled code through decoder to get a distribution over data samples
Code z를 Decoder에 통과시켜 data sample에 대한 분포를 구합니다.
*1번에서는 z에 관한 분포를 구한반면, 4번에서는 x에 관한 분포를 구합니다. 최종적으로 궁금한 것은 Original x의 분포이기 때문입니다.
5. Original input data should be likely under the distribution output from (4)!
원본 input 데이터는, 4번으로부터 나온 분포에 있을 likelihood가 높아야 합니다.
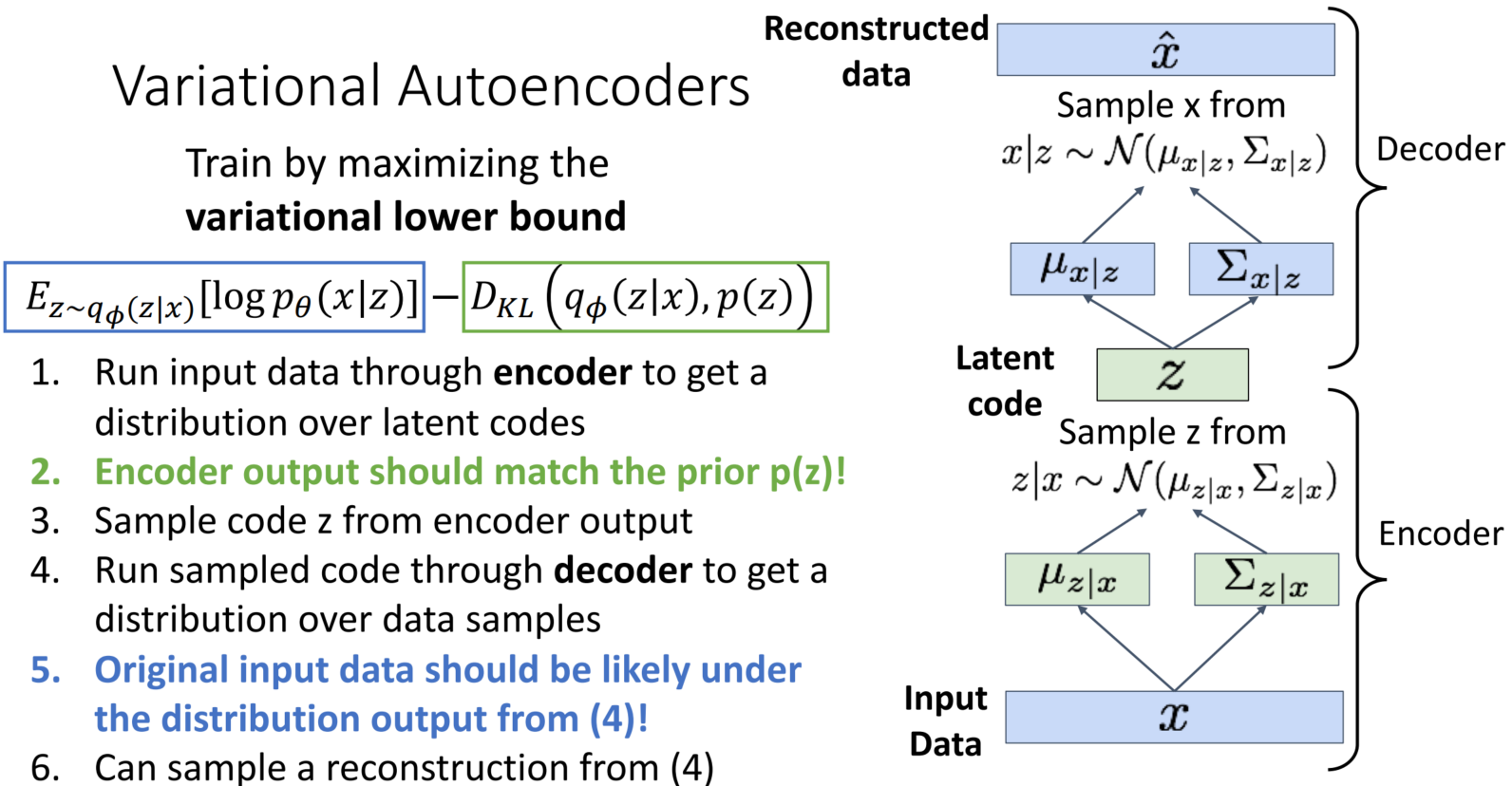
6. Can sample a reconstruction from (4)
4번에서 구한 분포로부터 sampling 하여 x_hat을 재구축합니다.
VAE: Generating
위의 6단계로 학습이 완료된 후에는, VAE로부터 데이터를 생성할 수 있습니다. Decoder만을 사용하여 새로운 데이터를 생성합니다.

1. Sample z from prior p(z)
2. Run sampled z through decoder to get distribution over data x
3. Sample from distribution in (2) to generate data

앞서 diagonal Gaussian으로 가정하였기에 z의 차원은 서로 독립입니다. 따라서 각 축들을 변경하여 생성하고 싶은 데이터를 수정할 수 있습니다.
*diagonal만 존재한다는 뜻은 자기 자신과만 관계를 맺는다는 뜻입니다.
VAE: Modifying
모델을 수정하는 단계는, 총 5단계로 이루어집니다.
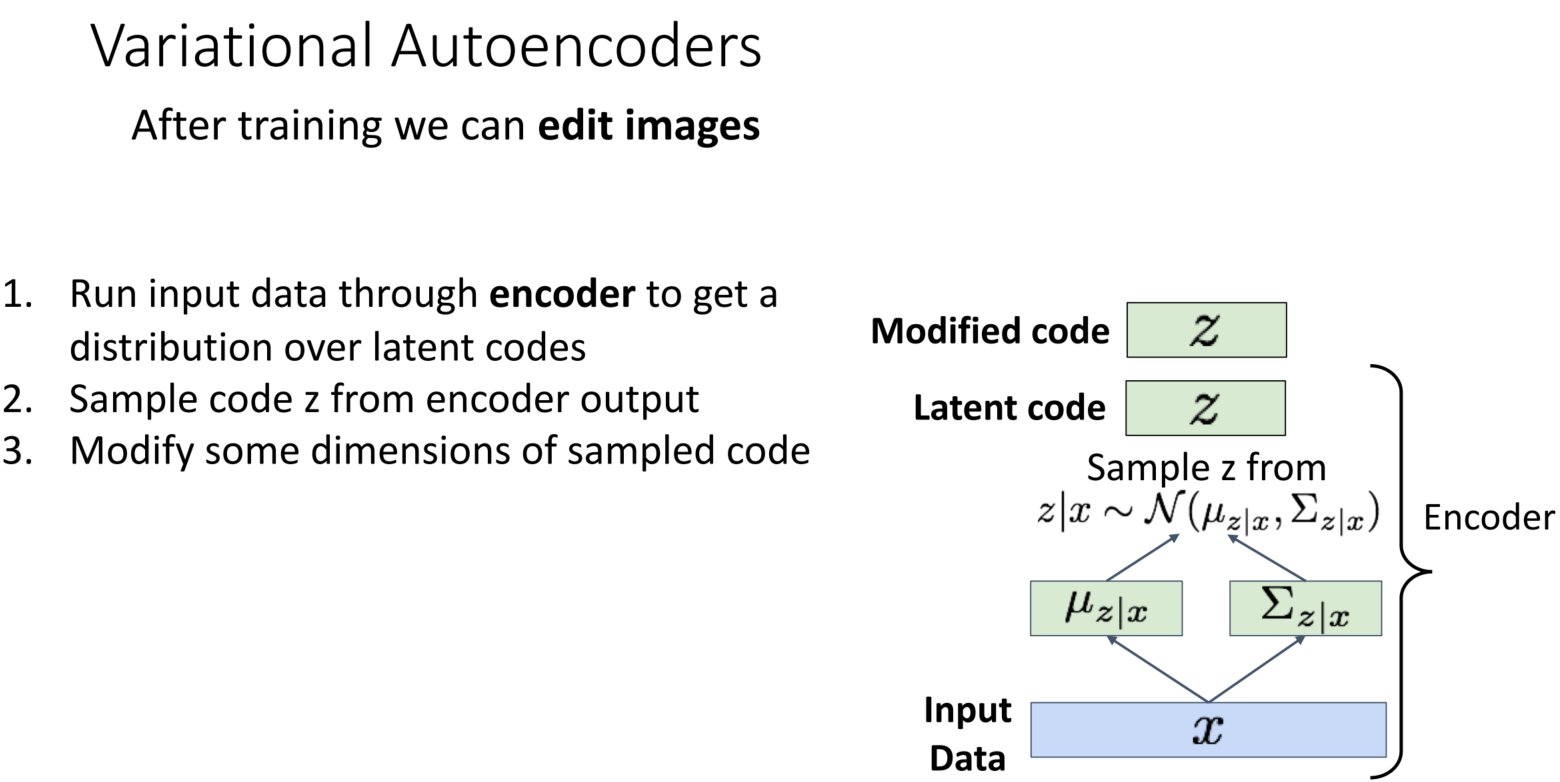
1. Run input data through encoder to get a distribution over latent codes
2. Sample code z from encoder output
3. Modify some dimensions of sampled code
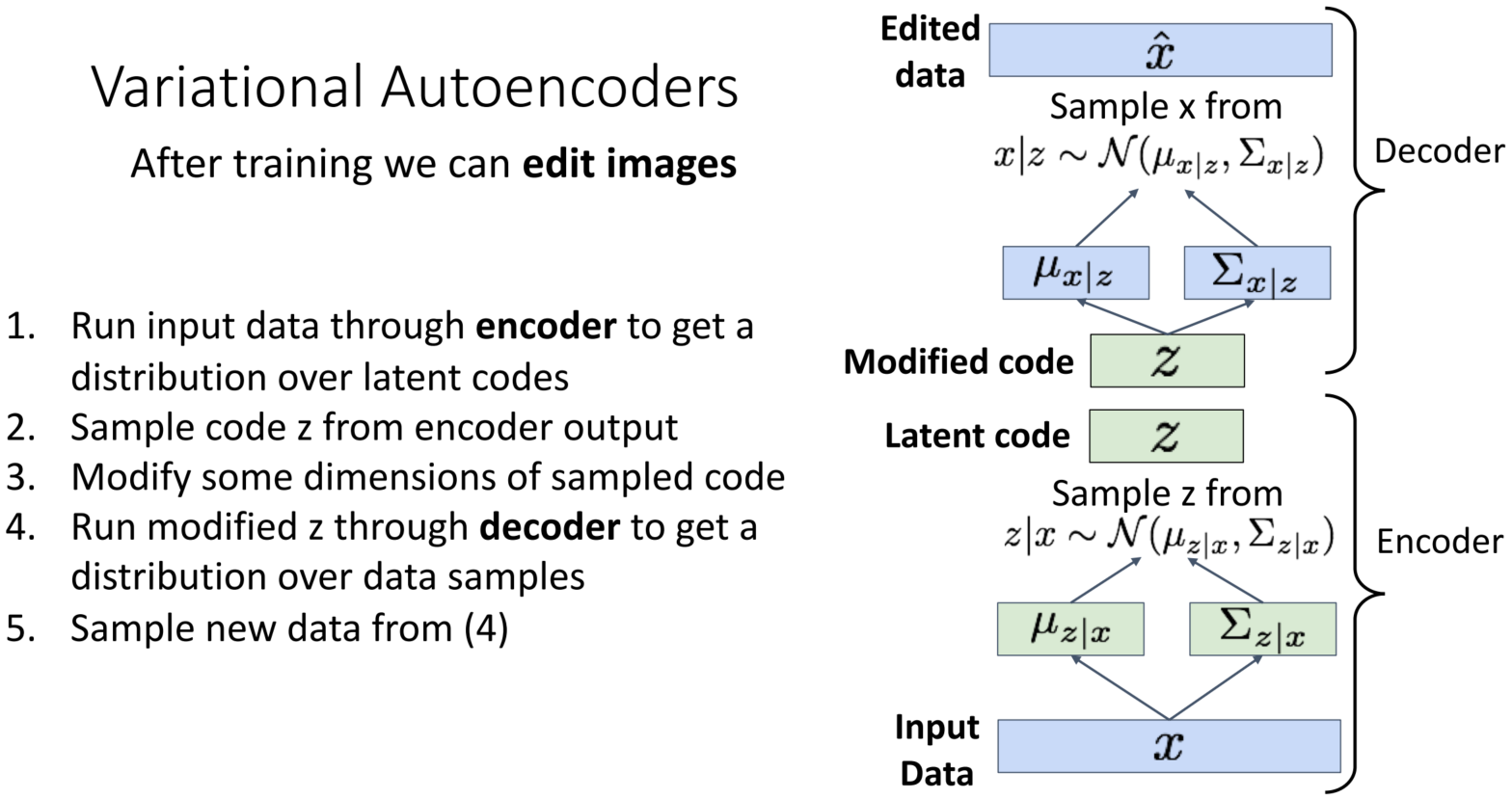
4. Run modified z through decoder to get a distribution over data samples
5. Sample new data from (4)
VAE: Summary

장점
- 생성 모델에 원칙적으로 접근함
- q(z|x)의 추론을 허용, 다른 작업에 유용한 feature representation
단점
- p(data)를 Maximize 하는 것이 아니라, lower bound를 Maximize 하기 때문에 Autoregressive보다 좋지 않음 SOTA(GANs)보다 품질이 좋지 않고, 흐릿함
VQ-VAE2: Vector-Quantized Variational Autoencoder

지금까지 배운 Autoregressive와 VAE는 각각의 장점을 지니고 있습니다. Autoregressive는 바로 p(data)를 최대화하고, 좋은 품질을 생성가능한 반면, 느리고 명확한 latent가 없다는 단점이 있습니다. 반면 VAE는 Autoregressive가 지니지 못한 장점들을 지니고 있습니다. 그럼 이 둘을 결합하면 좋은 모델이 만들어지지 않을까요?
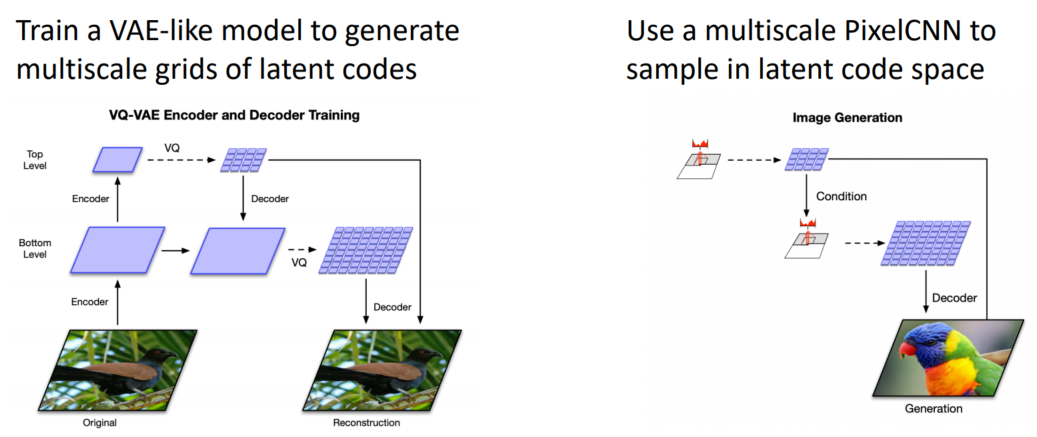
VQ-VAE2는 Autoregressive와 VAE의 장점을 결합하여 만든 모델입니다.

위의 이미지와 같은 고화질의 이미지를 생성할 수 있습니다.
GANs: Training
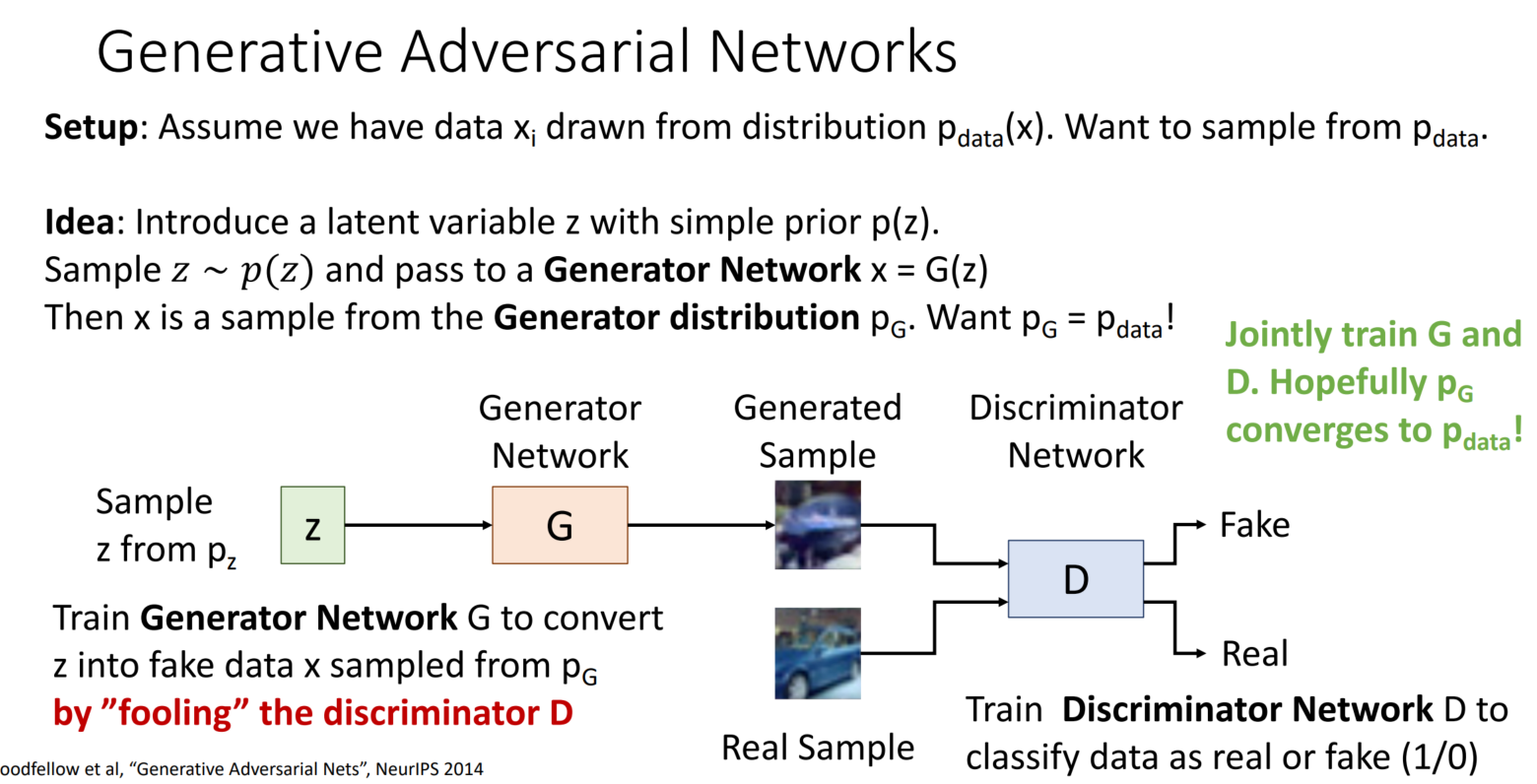
GANs은 다음과 같이 가정합니다. 분포 p_data(x)로부터 추출한 data x_i를 가지고 있을 때, p_data를 샘플링하고 싶습니다.
Idea: p(z)의 latent 변수 z를 도입합니다. p(z)를 따르는 z 샘플을 Generator Network x(=G(z))를 지나갑니다. 이는 x가 Generator 분포 p_G로부터 샘플링된 것을 의미합니다.
p_G = p_data를 만들고 싶습니다.
학습은 Generator와 Discriminator를 통해 진행됩니다. z를 p_G로부터 나온 fake 데이터로 변환하기 위해 Generator를 사용하고, Discriminator는 이를 잘 포착하는 방식으로 서로 학습합니다.
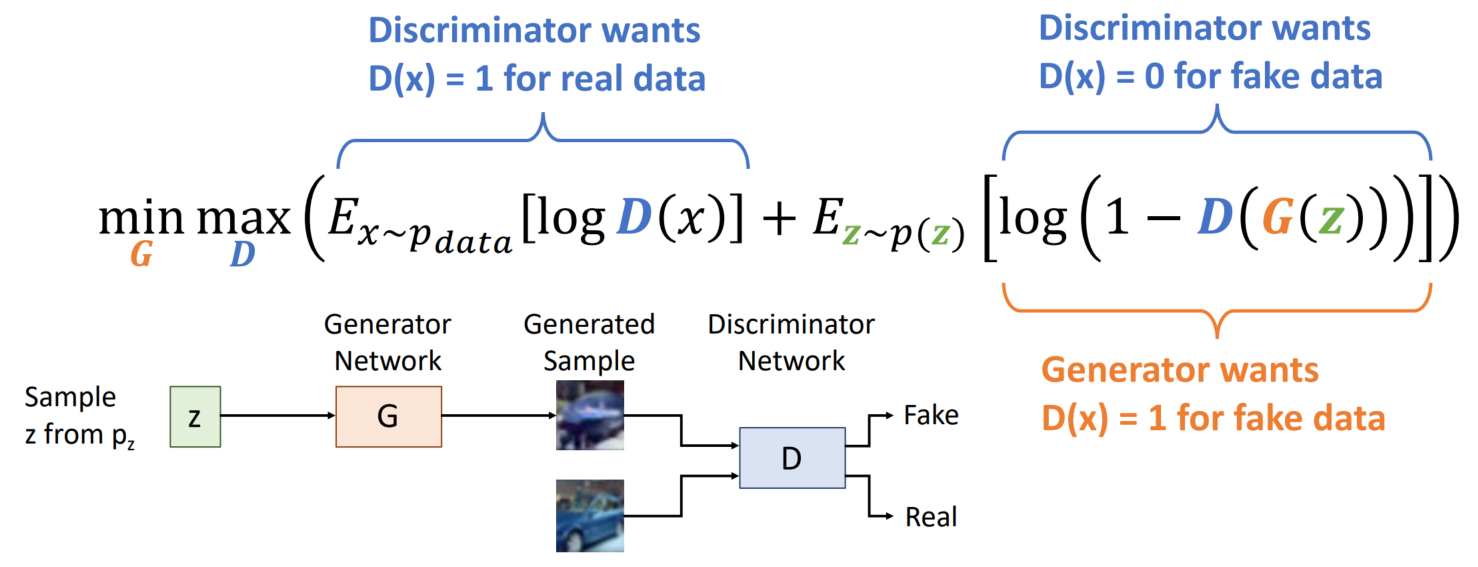
Generator를 max 하는 방향으로, Discriminator를 min 하는 방향으로 학습을 진행합니다.
첫 번째 항에서 Discriminator는 D(x)=1이 되기를 희망합니다. 즉 real 데이터를 선택하였음을 의미합니다. 두 번째 항에서 Discriminator는 D(x)=0이 되기를 희망합니다. 즉 Generator로부터 생성된 fake데이터를 선택하지 않음을 의미합니다. 반면 Generator는 Discriminator가 fake 데이터를 real 데이터와 구분하지 못하는 방향으로 나아가기를 희망합니다.
GAN을 쉽고 빠르게 이해하도록 도와주는 글이 있어 공유합니다.
* 경찰(Discriminator) vs 위조지폐범(Generator) 예시를 읽기를 추천드립니다
https://www.samsungsds.com/kr/insights/generative-adversarial-network-ai-2.html
[외부기고] [새로운 인공지능 기술 GAN] ② GAN의 개념과 이해
비지도학습 GAN(Generative Adversarial Networks)의 개념에 대해 쉽게 설명한 글입니다. 새로운 인공지능(AI) 기술 GAN에 대한 궁금증을 해결해 보세요.
www.samsungsds.com
GAN를 학습하는 방법에 대해 잠시 알아보겠습니다.

D는 gradient가 증가하는 방향으로, G는 gradient가 감소하는 방향으로 업데이트됩니다. 이때 전체 loss를 min 하는 것이 아니니, curve를 그릴 수 없습니다.
그럼 업데이트 방법을 살펴볼까요?
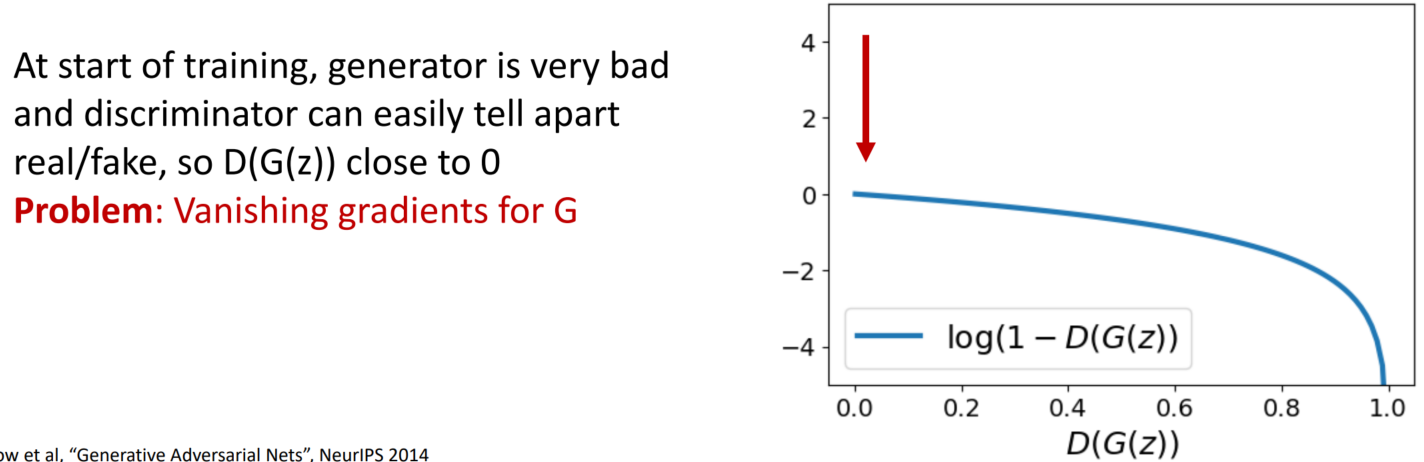
학습을 시작할 때는, G의 성능이 좋지 않아 D가 real/fake를 쉽게 구분할 수 있습니다. 즉 D(G(z))가 0에 가깝습니다. 여기서 문제가 발생합니다. 바로 G의 Vanishing gradient 문제입니다. 0에 가깝게 시작하다 보니 gradient가 업데이트가 이루어지지 않습니다.
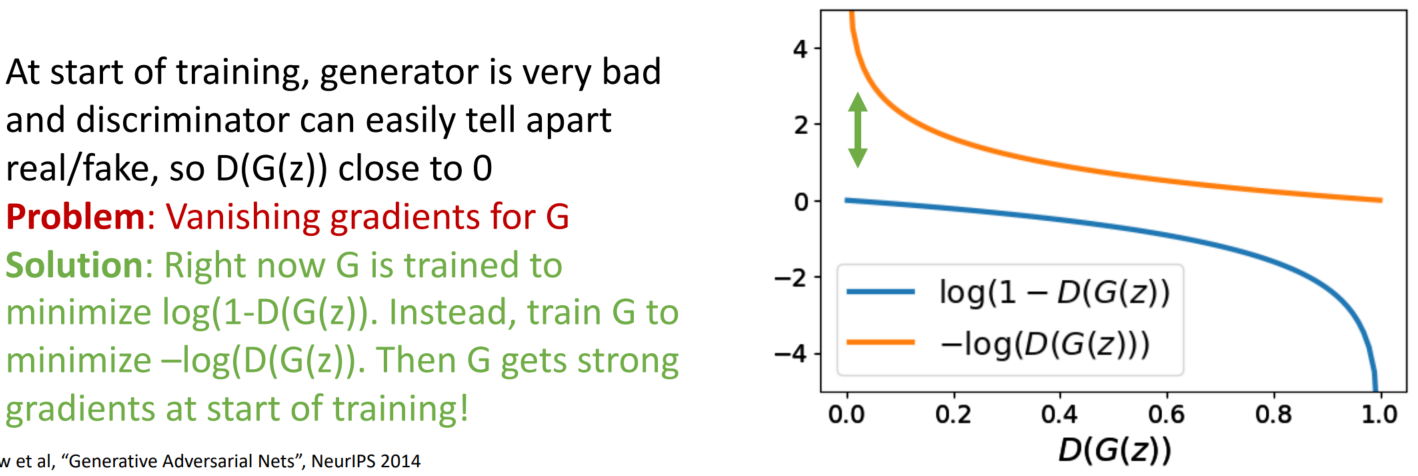
다음과 같이 식을 변경하여, Vanishing gradient 문제를 해결합니다.
min) log(1-D(G(z)) → min) –log(D(G(z))
GANs: Optimality
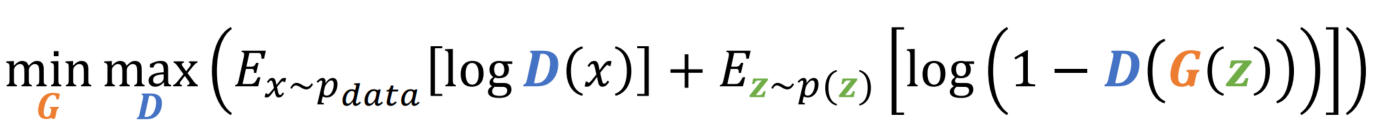
학습에서 가장 중요한 것 중 하나가 최적값이 어디인지 확인하는 것입니다. 지금부터 살펴보겠습니다.
미리 말하자면, GANs는 p_G = p_data일 때 전역 최솟값을 가집니다. 생각해 보면 당연한 것입니다. real / fake가 동일하다면 완벽히 복제한 것일 테니까요.
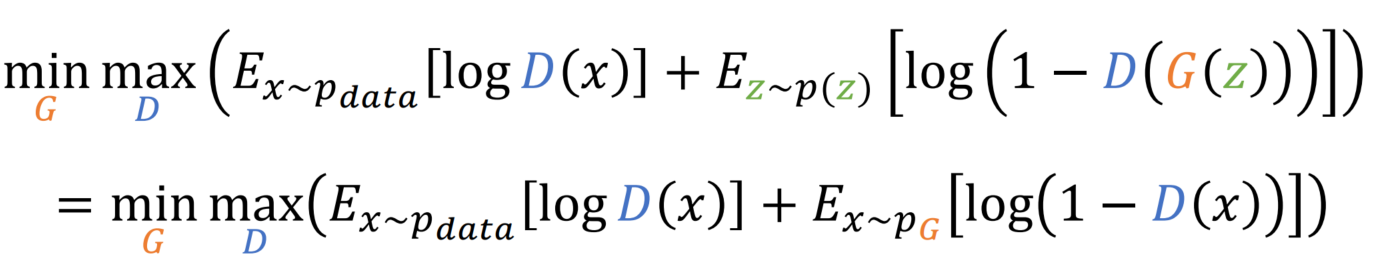
두 번째 항의 변수를 바꿔줍니다.
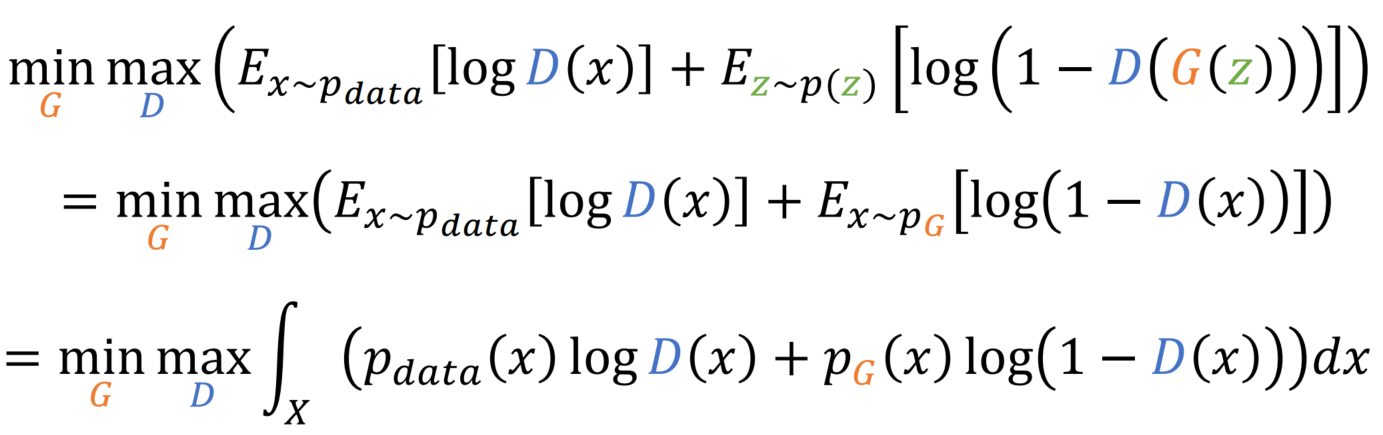
E(x) = sum(x * p(x))을 활용하여 integral과 p를 활용한 식으로 변경합니다.
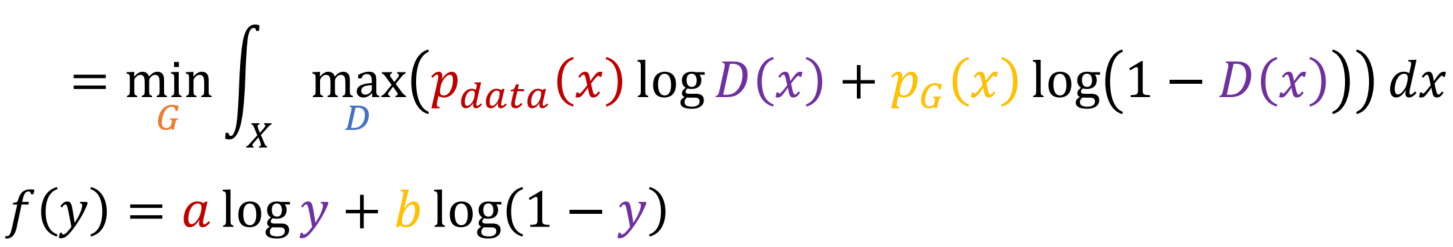
max D를 integral안으로 옮기고, max 내부의 함수를 f(y)로 표기할 수 있습니다.
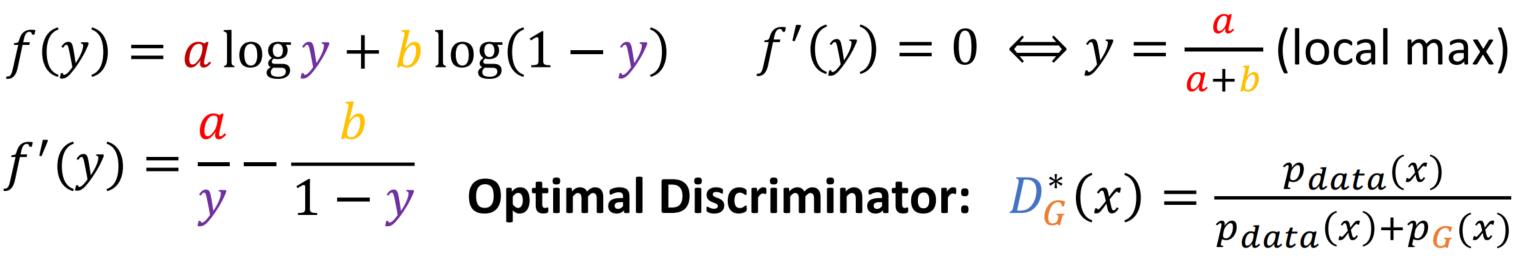
f(y)를 미분하여 언제 local max가 성립하는지 확인가능합니다. 이를 원래 식으로 바꾸면 언제 D가 Optimal인지 확인가능합니다.
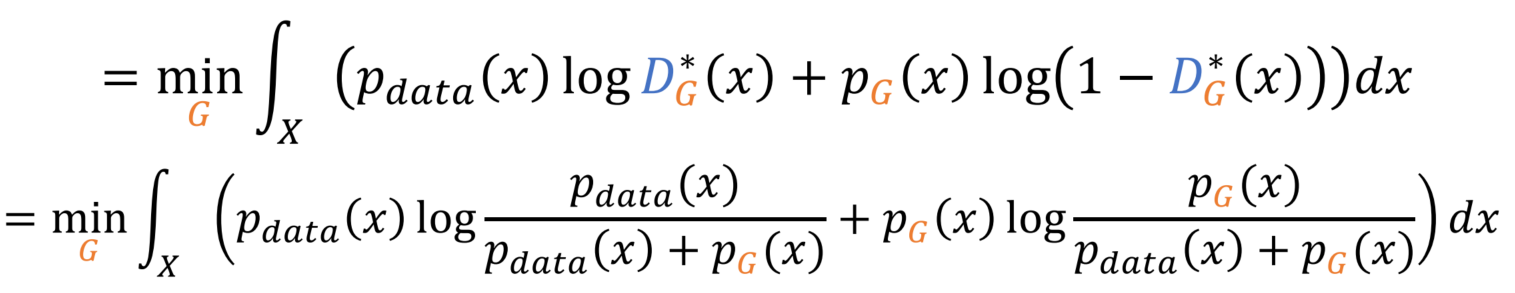
D의 Optimal일 때의 값을 대입하면, G에 관한 식으로 바뀌었습니다.
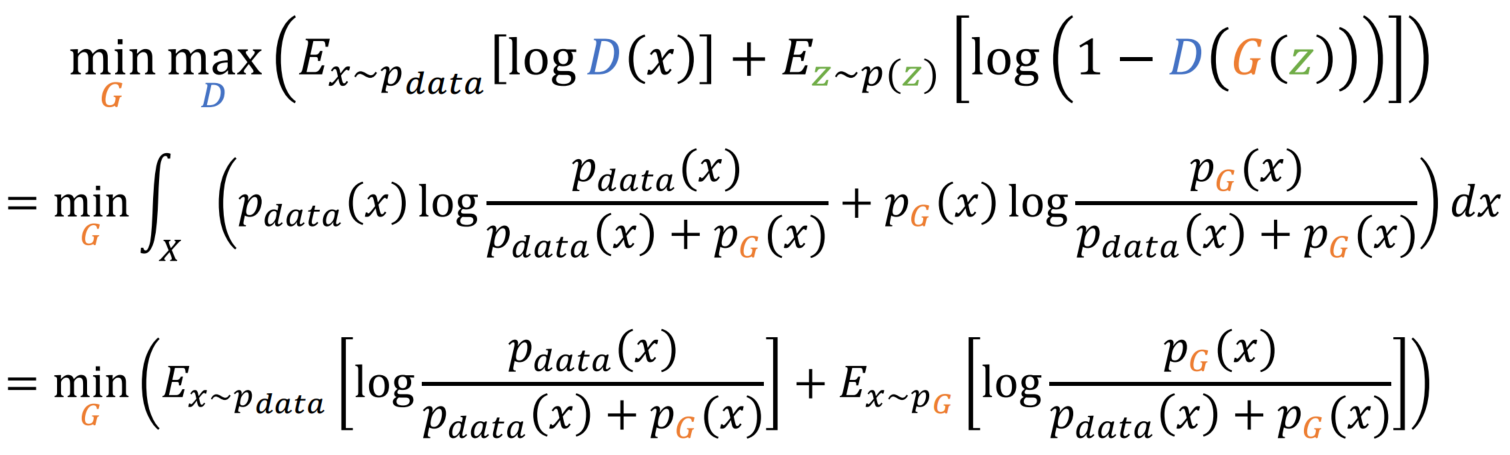
이전과 반대로 sum(x * p(x)) = E(x) 방향으로 식을 전개합니다.
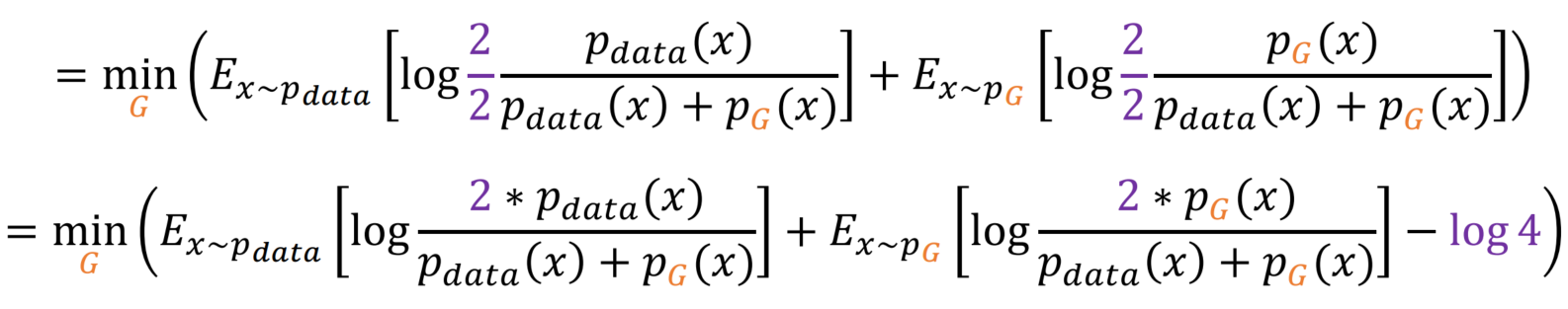
2/2를 곱하여 식을 위와 같이 변형합니다. 이는 Divergence를 활용하기 위해 사용되었습니다.

KL Divergence로 바꿔줍니다.
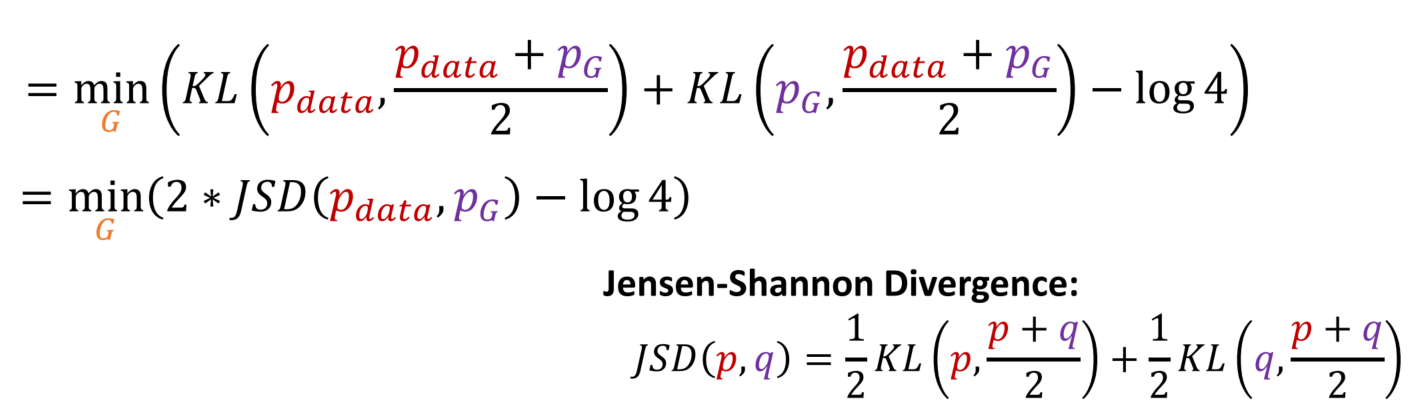
JSD로 한번 더 바꿔줍니다.
JSD는 항상 0보다 크거나 같습니다. 두 분포가 정확히 같을 때만 JSD=0이 성립합니다. 즉, p_data = p_G일 때 전역 최솟값이 됩니다.

단점
1. Generator, Discriminator는 고정된 크기의 neural net 구조입니다. 따라서 최적의 Generator, Discriminator를 표현하는지 보장할 수 없습니다.
2. 최적해로의 수렴에관한 어떠한 정보도 주지 않습니다.
GANs: DC-GAN
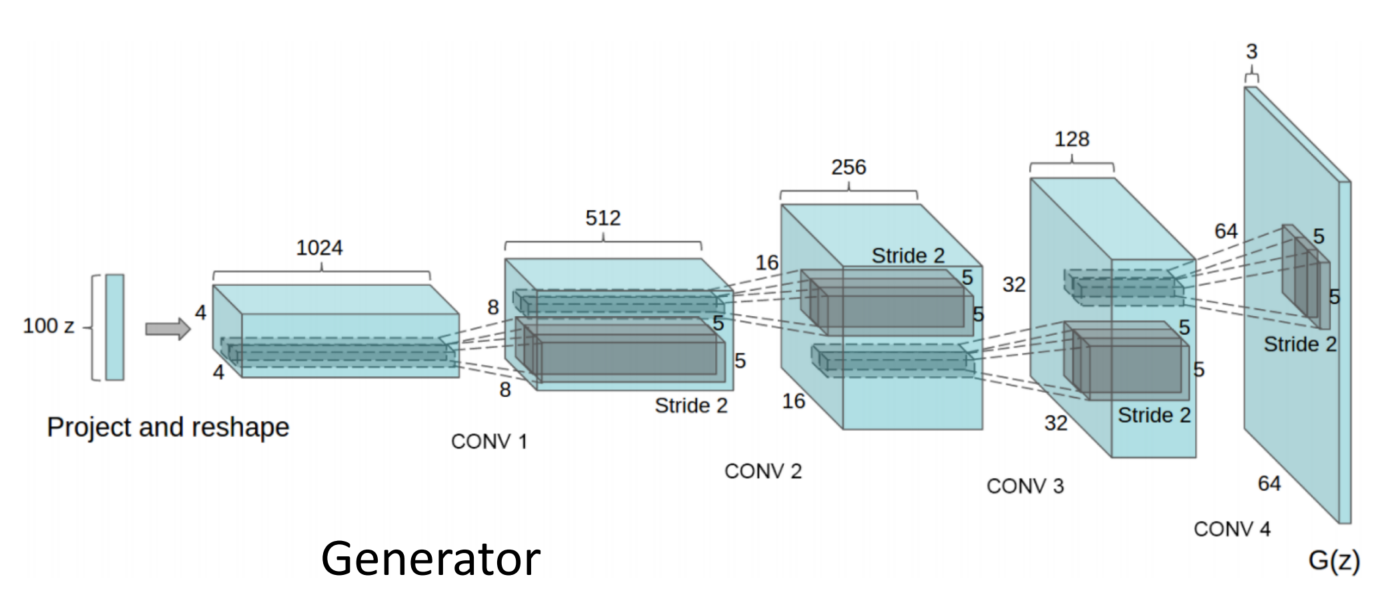
GANs: Vector Math


GANs: Conditional GANs
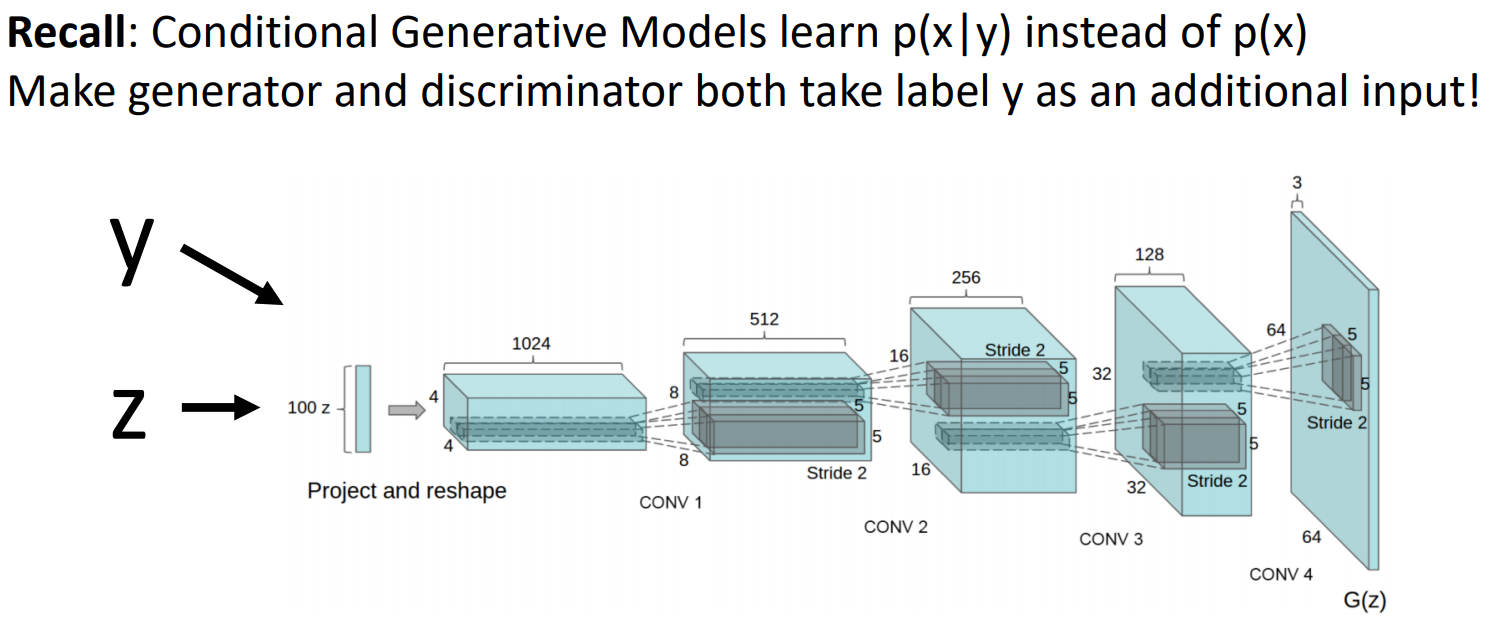
지금까지 본 GAN은 unconditional로 p(x)를 학습하였습니다. 즉 데이터셋을 통해 random sample을 생성하였습니다. Conditional GAN은 생성하고자 하는 sample type을 control 하기 위해 p(x|y)를 학습합니다. 기존의 GAN은 Generator에 random nosei z만 입력하였다면, Conditional GAN은 z와 함께 label(y)도 Generator에 입력합니다.
요약하자면 DC-GAN은 random sample을 생성(제어 x)하지만, C-GAN은 Generator에 label 정보를 함께 입력하는 방법을 통해 sample을 제어할 수 있습니다.
*이때 label 정보를 준다는 뜻은, 말 그대로 데이터가 지닌 label 정보만을 주는 것입니다

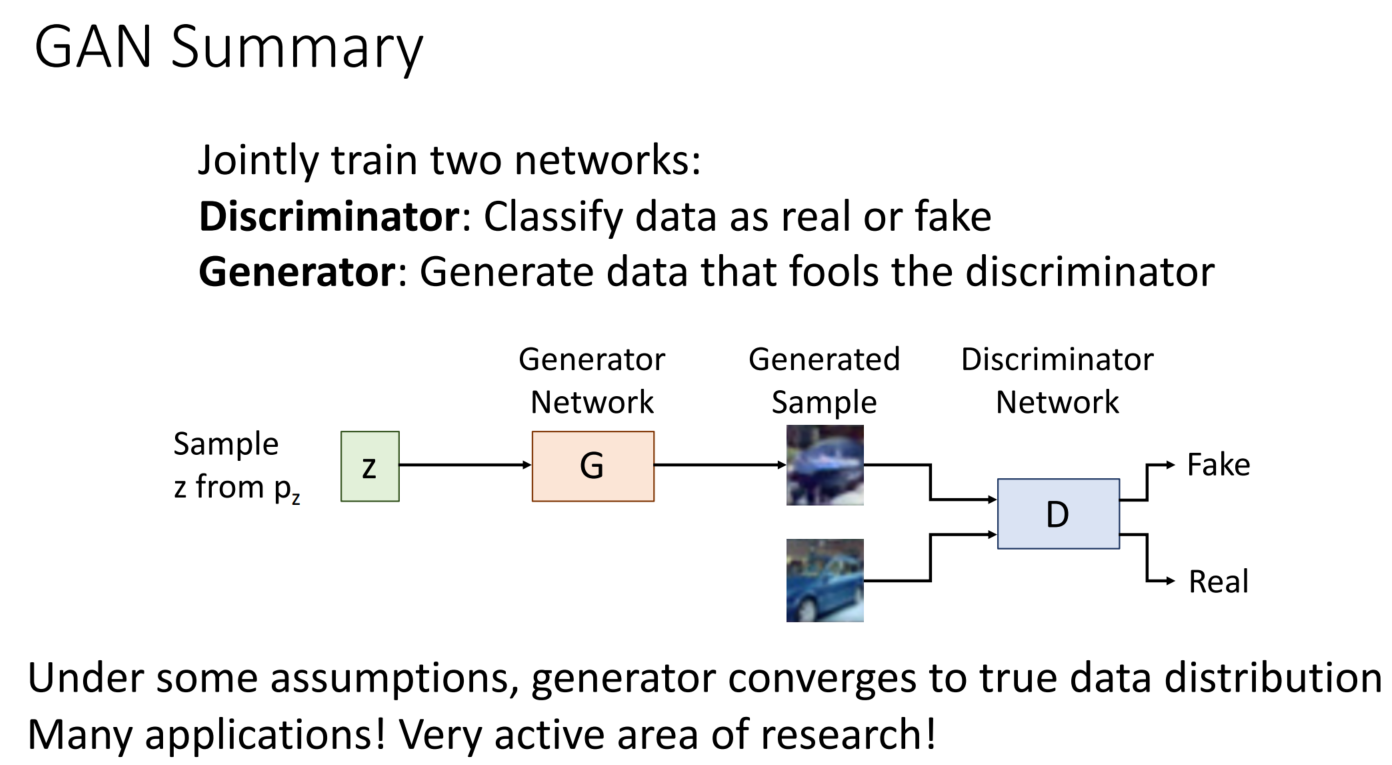
GANs: Summary
'공부 정리 > Machine learning & Deep learning' 카테고리의 다른 글
| [EECS 498-007 / 598-005] Lecture 19: Generative Models I (0) | 2023.02.15 |
|---|---|
| [EECS 498-007 / 598-005] Lecture 13: Attention (0) | 2023.02.09 |
| [EECS 498-007 / 598-005] Lecture 12: Recurrent Neural Networks (0) | 2023.02.08 |
| [EECS 498-007 / 598-005] Lecture 11: Training Neural Network (0) | 2023.02.01 |
| [EECS 498-007 / 598-005] Lecture 8: CNN Architectures (0) | 2023.01.26 |



