- 본 게시글은 MST-GAT: A multimodal spatial–temporal graph attention network for time series anomaly detection 정리글입니다.
- 개인적인 생각이 서술되어 있습니다. 잘못된 내용이 존재할 확률이 존재하기에 주의 바랍니다.
- 잘못된 내용, 오타는 지적해 주시면 감사하겠습니다.
Reference
- Ding, C., Sun, S., & Zhao, J. (2023). MST-GAT: A multimodal spatial–temporal graph attention network for time series anomaly detection. Information Fusion, 89, 527-536. / APA style
ABSTRACT
MTS(Multimodal time series) 이상치 탐지는 다양한 modality를 지니며 다변량 시계열 특징을 보이는 장치(ex: 수처리 시스템, 우주선)의 안전과 안정성을 유지하는 데 매우 중요합니다. 최근의 딥러닝은 이상치 탐지에서 잠재력을 보여주지만, 다른 modalities의 단변량 시계열 사이의 공간-시간(spatial–temporal) 관계를 명확하게 포착하지 못합니다. 그리고 이는 False negatives & False positives를 만듭니다.
본 논문에서는 이 문제를 해결하기 위해 MST-GAT(Multimodal Spatial-Time Graph Attention Network)을 제안합니다. MST-GAT은 먼저 M-GAT(Multimodal Graph Attention Network)와 시간 Convolution Network를 사용하여 다중 모드 시계열에서 공간-시간 상관관계를 포착합니다. 구체적으로, M-GAT은 modal 상관관계를 명쾌하게 모델링하기 위해 multi-head attention module과 두 개의 relational attention modules을 사용합니다. 또한 MST-GAT은 재구축 및 예측 모듈을 동시에 최적화합니다. 4가지 multimodal 벤치마크에 관한 실험 결과는, MST-GAT 기존의 SOTA보다 우수함을 보여줍니다. 추가 분석에 따르면 MST-GAT는 가장 변칙적인 단변량 시계열을 찾아 감지된 변칙의 해석력을 높입니다.
한 줄 요약: MTS 이상치 탐지는 특정 영역에서 매우 중요하다 → 딥러닝은 잠재력이 있지만, risk가 있다 → SOTA를 능가하는 MST-GAT을 제안하고자 한다!
1. Introduction
이상치 탐지의 하위 분야인, MTS 이상치 탐지에 중점을 둡니다. MTS 이상치 탐지는 산업용 장치 및 정보 기술 시스템 센서의 diverse modalities(예: 온도, 속도 및 전력)을 모니터링하는데 일반적으로 사용되며, 각 센서의 데이터 스트림은 단변량 시계열로 표시됩니다. 각 modality를 통해 탐지 불가능한 이상치를, Multimodal 시계열 데이터는 탐지 가능하게 합니다.
*Multimodal은 센서 간의 교호작용을 고려하기에 가능하다고 생각합니다, T-Square 등을 통해 여러 변수를 종합적으로 고려하는 것과 유사하다고 받아들였습니다
기존에는 숙련된 엔지니어가 수동으로, 고정된 이상치 기준을 설정하였습니다. 그러나 데이터 크기가 기하급수적으로 증가함에 따라 이 방법은 많은 노동력이 요구되었고, 또한 multimodal 한 상황이라면 각 센서에 대한 최적 기준선 설정이 매우 어려워졌습니다. 많은 이상치 탐지 방법이 이 문제를 해결하기 위해 제안되었으며, 단변량 시계열 데이터를 통한 탐지 결과를 종합하여 결론을 도출하였습니다. 하지만 multimodal 시계열 entity는 상호 연결된 단변량 시계열을 포함하며, 이러한 센서 데이터는 일반적으로 복잡한 비선형 방식으로 상관됩니다. 따라서 단변량 시계열로는 entity의 전반적인 상태에 대응하지 못하며, 여러 단변량 시계열 탐지 결과를 단순히 결합하는 방법은, 성능이 떨어지는 경향이 있습니다. 다중 모드 시간의 복잡한 공간 종속성, 시간적 종속성으로 인해 MTS 이상치 탐지가 어려웠습니다. 게다가 multimodal 시계열에는 동일한 modality 사이의 상관관계뿐만 아니라, 다른 양식의 시계열 간 상관 관계도 있습니다.
한 줄 요약: 이상치 탐지의 변천사(엔지니어의 경험에 의존 → 단변량 → 단변량 종합... but 문제가 있다, MTS도 마찬가지이다)
이전에는 MTS 이상치 탐지를 위해 SVR(Suppor Vector Regression), Bayesian models, ARIMA(autoregressive integrated moving average) 및 RNN 기반 모델을 포함하여 시간 종속성을 고려했습니다. 이러한 방법은 시간적 차원의 동적 변화를 확인할 수 있지만, 서로 다른 시계열 간의 공간적 종속성을 무시합니다. 공간적 관계를 고려하기 위해 몇몇의 연구는 CNN을 도입합니다. 그러나 CNN은 주로 이미지, 언어 데이터에 사용되기에 그래프 데이터에는 적합하지 않습니다. GNNs이 더 효과적입니다. GNNs와 GRU를 활용한 방법도 있고 이들은 유익한 진전을 이루었습니다. 그럼에도 이전 방법들은 multimodal 상관관계를 명확하게 포착하지는 못하였습니다.
한 줄 요약: MTS-GAT 이전에도 연구들은 진행되었지만, 다소 문제가 있었다.
MST-GAT은 multimodal 시계열 데이터 사이의 의존성을 분명하게 포착하기 위해 GATs를 채택합니다. 구체적으로, multimodal 시계열 간의 공간 종속성을 포착하기 위해 multihead attention module과 두 개의 relational attention modules을 포함하는 M-GAT를 만듭니다. Multimodal 시계열에서 서로 다른 관계를 명시적으로 모델링하면, 입력 데이터의 더 나은 기능 표현을 얻는 데 도움이 됩니다. 그런 다음 표준 컨볼루션 작업을 통해 각 시계열의 시간 종속성을 포착하기 위해 시간 컨볼루션 네트워크를 도입합니다. 또한 재구성 모듈과 예측 모듈을 공동으로 최적화하여 장점을 통합합니다. 재구축 모듈은 입력 데이터를 재구축하는 반면, 예측 모듈은 다음 타임스탬프의 특징을 예측하는 것을 목표로 합니다. 재구축 확률과 예측 오류는 감지된 이상을 설명하는 데 주로 사용됩니다.
본 논문의 특징은 다음과 같습니다.
- MTS 이상치 탐지 방법인 MST-GAT를 제안합니다. MST-GAT는 multimodal 시계열 데이터의 시공간 종속성에 관한 명시적 모델링 탐색을 개척합니다.
- VAE 기반 재구축 모듈과 MLP 기반 예측 모듈의 장점을 통합합니다. MST-GAT은 가장 높은 F1-score, 최고의 AUC을 달성하였습니다.
- MTS 이상치 탐지를 위한 효율적인 해석 방법을 고안합니다. 또한 이는 우리의 직감과 일치합니다.
한 줄 요약: MTS-GAT은 시공간 종속성도 잘 표현하고, 해석력도 좋다.
2. Related works
2.1. Time series anomaly detection
전통적인 이상치 탐지 기법은 클러스터링, 거리 기반, 밀도 기반, 격리 기반으로 분류할 수 있습니다. 최근 딥러닝 접근법도 관심을 받고 있습니다. 기존의 딥러닝 방법은 재구성 기반 방법과 예측 기반 방법으로 분류할 수 있습니다.
재구축 기반 기법은 전체 시계열의 잠재적 분포를 학습합니다. 다음 몇 가지를 살펴보겠습니다.
- DAGMM( Deep autoencoding Gaussian model)은 Deep Autoencoder 네트워크와 Gaussian 혼합 모델(GMM)을 결합하여 저 차원 feature와 재구축 기반 이상치 점수를 얻었습니다.
- OmniAnomaly는 VAE를 end-to-end 구조로 사용하여 입력 데이터를 재구축하고, 확률에 따라 이상 징후를 탐지했습니다.
- RAMED는 다중 해상도 네트워크를 활용하여 재구축된 출력이 입력의 전체 시간적 모양과 일치하도록 장려했습니다. 예측 기반 방법은 예측 잔차에 따라 다음 타임스탬프 및 이상 징후의 값을 예측합니다.
- Hundmanet al는 우주선 이상을 감지하는 LSTM의 가능성을 입증했으며, 주석에 의존하지 않고 동적으로 임계값을 설정하는 접근 방식을 도입했습니다.
- GDN(Graph deviation network)은 다변량 시계열에서 구조 학습을 수행하기 위해 GAT를 활용하고, attention 가중치로 감지된 이상을 해석했습니다.
이전 작업들은 재구축 기반 및 예측 기반 기법이 서로 다른 시나리오에서 보완적임을 입증했습니다. 따라서 이 두 패러다임의 장점을 통합하기 위한 공동 네트워크를 제안합니다.
그럼에도, 기존 방법 중 어느 것도 multimodal 데이터 간의 관계를 명시적으로 포착하는 것을 고려하지 않습니다. 따라서 multimodal 시계열 내에서 공간-시간 종속성을 명시적으로 구성하기 위해 multimodal 그래프 attention을 사용하여 이 문제를 해결하는 것을 목표로 합니다.
한 줄 요약: 재구축을 중점적으로 전통적인 이상치 탐지 기법 소개, 재구축 & 예측 기법 모두 좋다. 그러나 이를 통합하는 것은 제시되지 않았기에 우리가 해결해 보겠다.
* 이상치 탐지 기법이 궁금하신 분은 고려대학교 김성범 교수님의 강의를 참고하시길 바랍니다

이미지 출처: 고려대학교 김성범 교수님(DMQA) 강의자료
2.2. Graph neural networks
GNN은 소셜 네트워크, 의료와 같은 그래프 구조에서 두드러진 성공을 거두었습니다. 전형적인 GNN에서 노드는 인접 노드의 영향을 받습니다. GCN(Graph convolutional networks)는 spectral, spatial 방법이 포함됩니다. 하지만 spectral 방법은 의존 문제를, spatial 방법은 shift-invariance(이동 불변) 부족의 제한을 지니고 있습니다.
어텐션 메커니즘은 sequence-to-sequence 모델에서 효과적이고 널리 사용되는 구성 요소인데, 최근에는 그래프 신경망에 도입되었습니다. GAT는 aggregation 가중치를 이웃 노드에 할당하기 위해 어텐션 메커니즘을 활용했습니다. GAT의 관련 변형은 시계열 모델링과 관련된 작업 및 시계열 예측에서 진전을 이루었습니다. GAT는 유향 그래프(방향을 가진 그래프)에서 GCN보다 공간적 특징을 더 잘 추출할 수 있으며, 우수한 성능을 보여줍니다. GAT는 입력 특징 벡터 ℎ를, 어텐션 메커니즘을 활용하여 h'에 mapping 합니다. 어텐션 점수는 다음과 같이 수식화 됩니다.

- N_i는 인접 노트 집합
- a_ij hat은 정규화 이전의 노드 i, 노드 j 사이의 어텐션 점수
- 파이는 노드 간의 상관관계를, W는 가중치 matrix
- h_i는 노드 i의 특징을 나타내고, 활성화 함수로는 LeakyReLU를 사용
각 노드의 Output feature는 다음과 같이 계산되고, 여기서 시그마는 sigmoid 활성화 함수를 나타냅니다.

한 줄 요약: 어텐션 메커니즘을 그래프에 도입 ☞ GAT! +GAT에 관한 설명
*어텐션 메커니즘은 'Attention Is All You Need' 논문 이후 주목받게 되었습니다.
2.3. Multimodal machine learning
Multimodal 기계 학습은 다양한 양식의 정보를 최대한 활용하는 것을 목표로 합니다. 단일 modal 데이터를 사용하는 모델과 비교할 때, multimodal 데이터를 사용하는 모델은 항상 더 나은 성능을 보입니다. 다중 모드 정보를 통합된 표현으로 융합하는 방법은 주요 과제입니다. 다중 모드 기계 학습은 multi-kernel learning models, probabilistic graphical models, neural network models 등으로 구현할 수 있습니다. 이 중 neural network가 multimodal 데이터를 융합하는 뛰어난 능력으로 인해, 상당한 성능 향상을 가능하게 했습니다.
3. Methodology
3.1. Problem definition
MTS 이상치 탐지 모델은 타임스탬프 수준에서 이상을 감지하도록 설계되었습니다. 시계열 이상치 탐지는 일반적으로 비지도 학습으로 여겨지고, training phase에서는 이상치가 없다고 가정하고 학습을 진행합니다. Multimodal 시계열 데이터는 T 타임스태프가 있는 𝑁개의 단변량 데이터로 구성됩니다.
*일반적으로 Phase I에서 정상 데이터로만 학습 및 모델 생성, Phase II에서 이상치 탐지를 진행합니다.
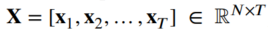
<Example>
3.2. Overview of MST-GAT
MST-GAT은 각 센서를 노드와 노드들의 관계를 엣지로 표현합니다. 복잡한 multimodal과 시공간관계를 전체 시계열에서 모델링합니다. 구조는 다음 4개의 파트를 포함합니다.
- Graph Structure Learning: 공간 차원에서 그래프 구조를 학습하기 위해 시계열 임베딩을 사용합니다.
- M-GAT(Multimodal Graph Attention Network): multi-head attention 모듈 및 additional relational attention 모듈을 사용하여 명시적으로 모드 내 및 모드 간 관계를 포착합니다.
- Temporal Convolution Network: 시간 축의 컨볼루션 구조를 활용하여 시계열의 시간 종속성을 포착합니다.
- Joint Optimization and Anomaly Score: MST-GAT은 재구축 및 예측 대상을 모두 최적화한 다음, 이상치 score로 이상치를 탐지합니다.
전체적인 구조는 다음과 같습니다.
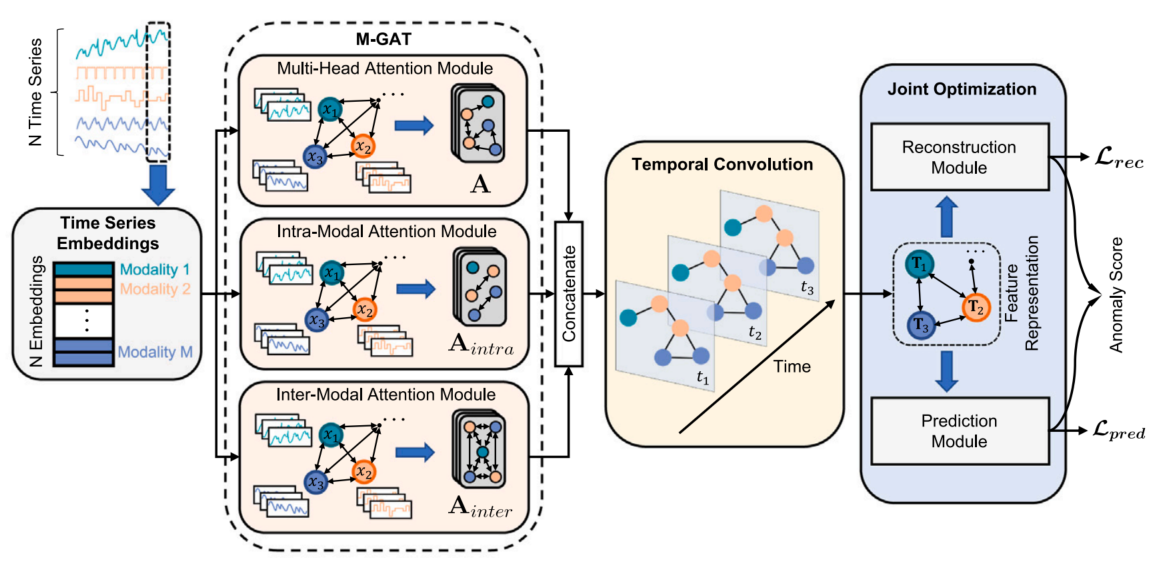
3.3. Graph structure learning
본 논문에서는 multi-head attention 모듈을 위한 유연한 그래프 구조를 구성하기 위해 시계열 임베딩을 소개합니다. Multimodal 시계열에 대한 𝑁 개의 노드(각 노드는 단변량 시계열을 저장합니다)가 있는 그래프 구조 C를 떠올려봅니다. 엣지(노드와 노드 사이)는 서로 다른 시계열 간의 종속성을 나타냅니다.
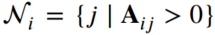
- 노드 i와 이웃해있는 노드들의 집합은 다음과 같이 표현됩니다.
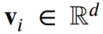
- 노드 i에 대한 임베딩 시계열은 우측과 같이 정의합니다. 여기서 i, d는 임베딩 차원입니다.
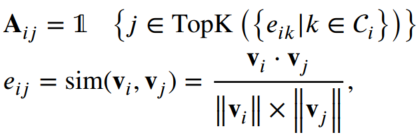
- 시계열 임베딩은 multi-head attention 모듈을 위한 인접 matrix A를 구성하기 위해 사용되고, A는 우측과 같이 표현됩니다. C_i에 j가 포함되어 있다면 A_ij = 1, 그렇지 않다면 A_ij = 0이 됩니다. sim()은 코사인 유사도를 표현합니다. TopK는 가장 큰 코사인 유사도를 지닌 K의 index를 표현합니다.
먼저, e_ij(임베딩 벡터 사이의 코사인 유사도)를 계산합니다. 다음으로 후보 집합에서 top K 유사한 노드를 선택합니다. 파라미터 k는 그래프 구조의 sparseness를 제어합니다.
3.4. M-GAT in spatial dimension
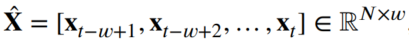
X hat은 M-GAT의 시점 t에서의 입력값을 의미합니다.
- w는 sliding window의 길이를 의미합니다.
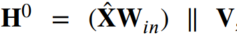
- M-GAT의 초기값은 우측과 같고, ||는 연속을 의미합니다.
M-GAT의 구조는 다음과 같습니다.
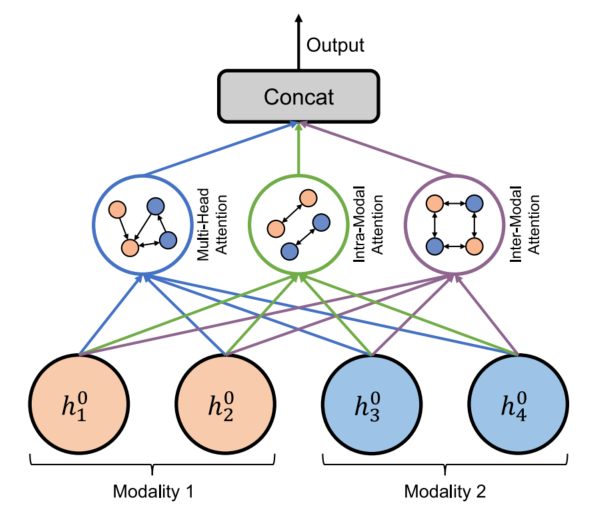
3개의 attention 모듈(multi-head attention, intra-, inter-modal attention)을 포함합니다.
- multi-head attention 모듈은modality-independent 공간 관례를 모델링하는 데 중점을 둡니다.
- intra- and inter-modal attention 모듈은 서로 다른 시계열 간의 multimodal 상관관계를 포착하는데 중점을 둡니다.
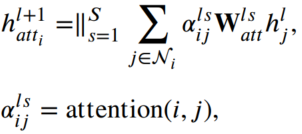
- Multi-head attention은 이웃과 합하여 노드를 업데이트 합니다. h는 H에 포함된 원소이고, layer l의 노드 j를 의미합니다. S는 # of attention heads, 알파는 attention score를 의미합니다.
한 줄 요약: mulit-head attention은 독립, intra- & inter-modal attention은 상관관계에 중점을 둔다
3.5. Convolution in temporal dimension
M-GAT에서는 인접 노드의 공간 차원 정보를 포착합니다. 반면 Temporal Convolution Network는 시간 차원에서 stand convolution을 통해 temporal dynamic을 포착합니다.
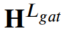
- Temporal Convolution Network의 입력값은 우측과 같고, L_gat은 M-GAT의 # of layer를 의미합니다.
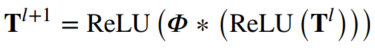
- Temporal-level 표현은 우측과 같이 계산됩니다. T**(l+1)은 later l+1에서의 시간 표현을 의미합니다.
3.6. Joint optimization and anomaly score
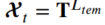
- 재구축 & 예측 모듈의 입력값은 temporal convolution network의 출력값과 동일합니다. 즉, 입력값은 우측과 같이 표현됩니다.
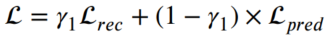
- MST-GAT에서는 두 과업을 최적화합니다. Loss function은 두 식을 포함하고, 우측과 같이 표현됩니다. 우변의 첫 번째 항은 재구축 손실 함수, 두 번째 항은 예측 손실 함수를 의미합니다.
그럼 각 항에 대해 살펴보겠습니다.
3.6.1. Reconstruction module
재구축 모듈의 목적은 입력값의 재구축 확률을 배우는 것입니다. VAE를 사용하였고, z는 잠재 표현입니다.
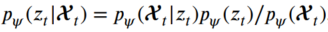
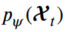
는 재구축 확률을 표현합니다. 다음과 같이 정의할 수도 있습니다.
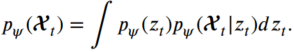
위 식은 계산이 어려우니 근사를 이용, 최종적으로 Encoder와 Decoder를 활용한 재구축 loss는 다음과 같이 정의합니다.
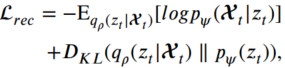
3.6.2. Prediction module
예측 loss는 다음과 같이 정의됩니다.
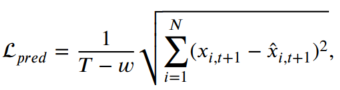
3.6.3. Anomaly score and inference
최종적인 이상치 score는 다음과 같습니다. 처음에 마주한 표현과는 다르지만, 기능은 동일한 것으로 생각됩니다.
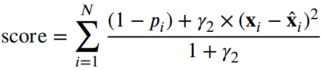
4. Experiments
이번 장에서는 주로 사용되는 공공 데이터를 소개한 다음, 이 데이터에 관한 MST-GAT 성능을 평가할 것입니다. 다음으로 Ablation study를 통해 중요한 요소를 판별할 것입니다. 마지막으로 case study를 통해 MST-GAT의 해석력을 보여줍니다.
*Ablation study: 한 개이상의 component 제거를 통해 component가 영향을 미치는 정도를 파악하는 방법

4.1. Datasets
- MSL, SMAP: 우주선에서 얻은 실제 데이터 셋으로, NASA 전문가가 주석을 달았습니다. Training set은 정상 데이터로, test set은 labeling 된 이상치 데이터를 포함하고 있습니다.
- SWaT: 7일간의 정상 작동과 4일간의 모의 공격 시나리오로 구성된, 51개의 센서가 있는 수처리 테스트베드에서 데이터 셋이 수집되었습니다.
- WADI: 123개의 센서로 구성된 감소된 물 분포 테스트베드에서 얻은 데이터 셋입니다. Training set은 정상 작동된 2주를, test set으로 공격 시나리오 2일을 포함합니다.
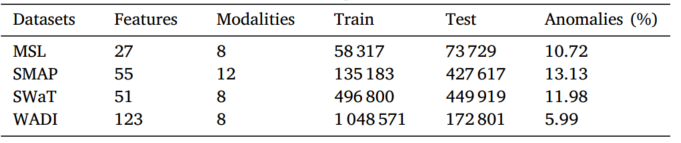
*MSL: Mars Science Laboratoryrover
*SMAP: Soil Moisture Active Passive satellite
*SWaT: Secure Water Treatment
*WADI: Water Distribution
4.2. Baselines
MST-GAT을 8가지의 MTS 이상치 탐지 기법과 비교했습니다. 두 그룹으로 나누면 다음과 같습니다.
1. Mono-modal 기법: PCA / AE / DAGMM / LSTM-VAE
2. Multi-modal 기법: MAD-GAN / OmniAnomaly / USAD / GDN
4.3. Evaluation metrics for MTS anomaly detection
Precision (Prec), Recall (Rec), F1-score (F1), and the area under the ROC curve (AUC)를 평가 지표로 사용하였습니다. 각 평가지표는 다음과 같습니다.

- Prec: 전체 이상치 중, 올바르게 탐지된 이상치의 비율입니다.
- Rec: 이상치로 탐지한 이상치 중, 올바르게 탐지된 이상치의 비율입니다.
- F1: Prec과 Rec을 종합적으로 고려한 지표입니다.
*해당 지표들은 분류문제에서 사용되는 지표들입니다.
4.4. Experimental setup
- CPU: Intel(R) Xeon(R) CPU E5-2640 @ 2.50 GHz
- GPU: NVIDIA 2080ti GPU
- Optimizer: Adam
- Learning rate: 1×10**−3
- Batch size & Epochs: 32 & 60
- Embedding dimension: 128
- Sliding window size & Kernel size: 32 & 16
- r_1 & r_2: 0.5 & 0.8
4.5. Results and analysis
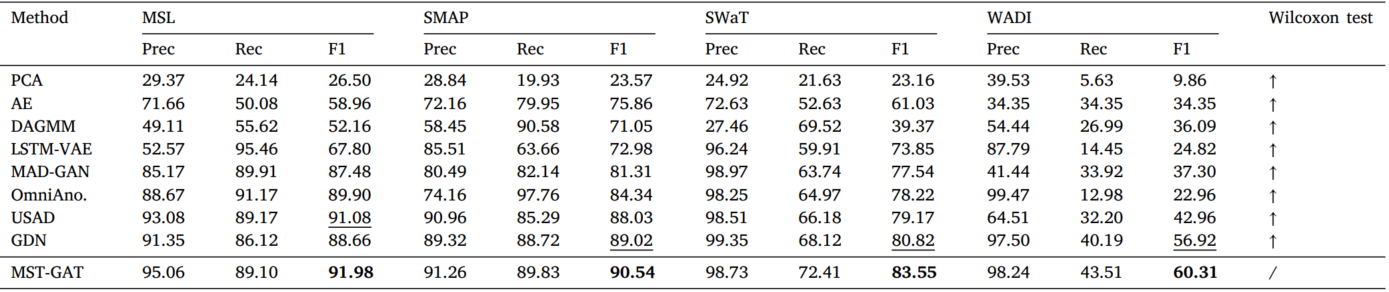
4개의 데이터 셋 모두에서 MST-GAT의 F1-score가 가장 높음을 확인할 수 있습니다. MSL과 SWAP은 상대적으로 간단한 이상치 패턴, 시공간 dymapics를 지니고 있기에 대다수 기법이 높은 점수를 보여줍니다. 반면, SWaT와 WADI에서는 대다수 기법이 낮은 점수를 보이는데, 더 복잡한 이상치를 포함하고 있기 때문입니다. 그럼에도 MST-GAT는 여전히 좋은 점수를 보이고 있습니다.
4.6. Ablation studies
MST-GAT의 각 구성 요소의 역할을 이해하기 위해 Ablation study를 진행하였습니다. 처음으로 intra- and inter-modal attention 모듈을 제고하였고, 두 번째로 temporal convolution을 제거하였습니다. 세 번째로는, 그래프 구조 학습을 연구하기 위해 TopK로 구현한 그래프를 complete 그래프로 대체하였습니다 (부분 사용을 전체 사용으로 대체하였음을 의미). 마지막으로 multi-head attention 모듈의 attention mechansim을 버리고, 각 이웃에 동일한 가중치를 할당하여 정보를 집계하였습니다(이웃별 달랐던 점수를, 동일한 점수로 바꿨음을 의미).
실험 결과는 다음과 같습니다.
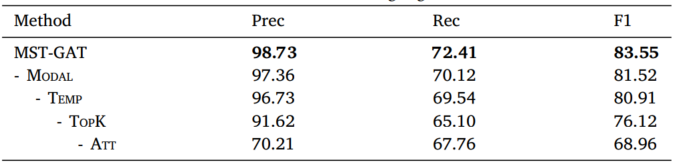
1. Intra- and inter-modal attention 모듈 제거는 상당한 성능 저하를 발생시켰습니다. 이는 multimodal 시계열에서 모드 내 및 모드 간 종속성을 명시적으로 포착하는 것이 성능 향상에 도움이 된다는 것을 나타냅니다.
2. Temporal convolution을 지닌 MST-GAT는 그렇지 않은 모델보다 성능이 우수합니다. 따라서 multimodal 시계열에서 시간 의존성을 모델링해야 합니다.
3. Attention mechanisms을 사용하지 않는 MST-GAT은 성능이 나쁩니다. 각 단변량 시계열은 매우 다른 속성을 가지므로, 동일한 가중치를 할당하면 노이즈가 발생하고 다중 모드 시계열의 복잡한 종속성을 모델링할 수 없습니다.
4. Component를 제거할 때마다 F1 score가 지속적으로 저하되는 것을 통해, MST-GAT에서 각 Component가 합리적이라고 말할 수 있습니다.
5. Conclusions
본 논문은, MST-GAT을 제안하였습니다. multimodal graph attention network와 temporal convolution network를 사용하여 공간적 상관관계와 시간적 종속성을 포착하였습니다. 제안된 모델은 재구축 및 예측 모듈을 활용하였고, 나아가 재구축 확률과 예측값을 기반으로 검출된 이상치에 대한 효율적인 해석 접근법을 제안하였습니다. 실험을 통해 MST-GAT은 현재의 SOTA를 넘어서고, 인간의 직관과 일치하는 해석 가능한 결과를 제공함을 확인할 수 있었습니다.
최종 정리: 일반적인 이상치 탐지 기법은 동일한 공정을 반복하는 공장처럼, 주로 process가 stationray 한 상황이고, 이때 활용가능한 기법들은 많다. 하지만 시간에 따라 변하는 MTS 한 상황에서는 좋은 기법이 없었다. 본 논문에서는, 시간-공간을 활용하여, 공간에서는 주로 사용되던 재구축을 attention을 사용하여 시계열 feature 간의 관계를 포착할 수 있었고, 시간에서는 예측을 통해 보정해 주는 느낌으로 진행되었다. 최종적으로 이 둘을 결합하여 이상치 score를 계산하였다. MST-GAT 이전에 주로 사용되던 기법은, 한 분야에서는 뛰어나지만 시간-공간을 종합적으로 고려한 기법은 아니기에 MST-GAT보다 모두 성능이 좋지 않다.
*각 노드에는 단변량 데이터의 feature를, 노드와 노드 사이의 엣지는 attention score를 활용하여 graph를 구축



