- 본 게시글은 Justin Johnson 교수님의 Deep Learning for Computer Vision, University of Michigan 정리글입니다.
- 개인적인 생각이 서술되어 있습니다. 잘못된 내용이 존재할 확률이 존재하기에 주의 바랍니다.
- 잘못된 내용, 오타는 지적해 주시면 감사하겠습니다.
강의링크:
https://www.youtube.com/watch?v=lGbQlr1Ts7w&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=10
강의자료:
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture10.pdf
Activation Functions

6강(Backpropagation)에서 다음과 같은 공식을 배웠습니다.
Downstream = Local x Upstream
그리고 Downstream은 다음 step의 Upstream이 되지요. 이를 염두에 두고 Multi Layer의 효과를 만드는 Activation Function을 배워보겠습니다.
Sigmoid

Sigmoid 함수는 [0,1] 범위를 가지는 함수로, saturating 상태를 가장 잘 나타냅니다. 하지만 3가지 문제로 인해 실제로는 사용하지 않습니다.
1. Saturated neurons “kill” the gradients
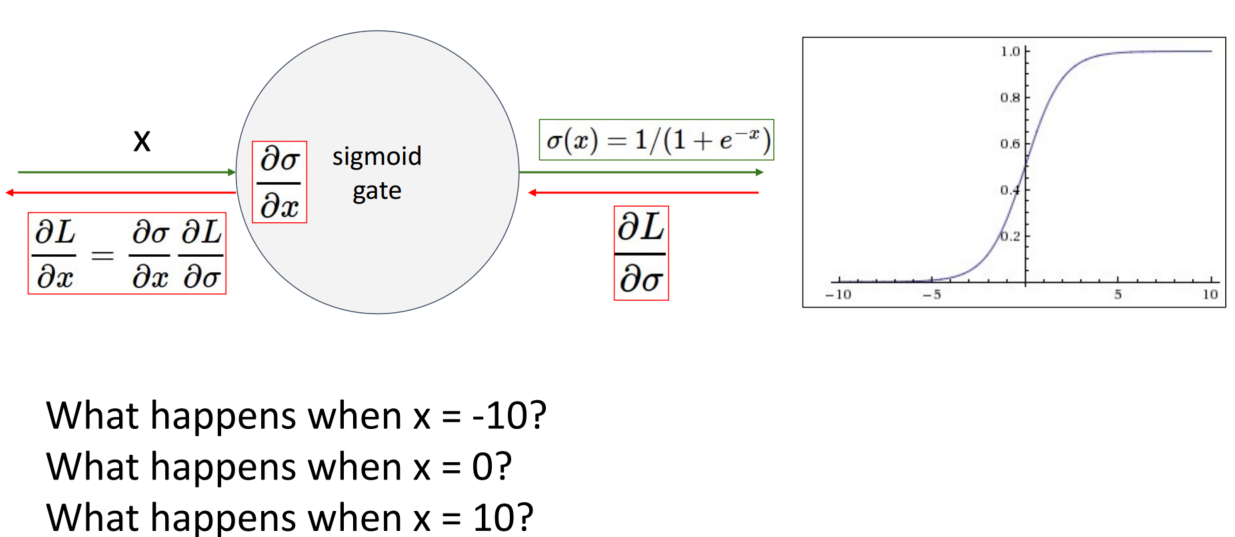
Sigmoid 함수는 x가 양 끝단에 가까워질수록 기울기(local gradient)가 0에 가까워집니다. Local이 0에 가까워질수록 Upstream이 크더라도 Downstream은 0에 가까워집니다. 그리고 이 Downstream은 다음 step의 Upstream이 되기에 step이 진행될수록 gradient가 0에 가까워지며 weight가 거의 update 되지 않습니다.
2. Sigmoid outputs are not zero-centered

Sigmoid 함수는 처음 input x의 부호에 따라 w_i에 대한 local gradient의 부호가 결정됩니다. 모든 weight들이 + or - 방향으로만 update 되기에 학습이 느려집니다. 다행히 실제로 학습을 할 때는 minibatch를 활용하여 학습하기에 이 문제는 개선됩니다.
3. exp() is a bit compute expensive
지수함수는 계산이 복잡하기에 연산이 느리다는 단점이 있습니다.
3가지 단점 중 가장 치명적인 단점은 1번 단점입니다.
Tanh

Tanh 함수는 Sigmoid 함수와 유사하게 생겼죠? Sigmoid와 다른 점은 Tanh 함수는 [-1, 1] 범위를 가지고, zero centered 되어있습니다. 그럼에도 여전히 gradient가 0에 가까워지는 문제를 지니고 있습니다. Sigmoid와 마찬가지로 실제로 사용하지는 않습니다.
ReLU

ReLU는 가장 대중적으로 사용되는 Activation Function입니다. x > 0 일 때는 기울기 소실 문제가 발생하지 않고, 계산이 편리하여 sigmoid와 비교할 때 6배 빠른 속도를 보입니다. 그럼에도 2가지 단점이 존재합니다.
1. Not zero-centered output
Sigmoid와 마찬가지로 not zero-centered output이기에 zig-zag 패턴을 보이는 단점이 있습니다.
2. Dead ReLU
x < 0 일 때의 기울기=0입니다. weight update가 전혀 이루어지지 않기에, 이때는 차라리 sigmoid가 좋습니다.

요즘에는 잘 사용하지 않지만 Dead ReLU를 회피하기 위해 positive bias를 추가하여 ReLU를 시작할 수도 있습니다. 그럼 gradient가 0에 수렴할 확률이 줄어들기 때문입니다.
Leaky ReLU

ReLU는 x < 0 일 때 기울기=0인 문제가 존재했습니다. Leaky ReLU는 x < 0일 때 f(x) = 0.01x로 설정하여 weight update가 이루어지지 않는 문제를 해결하였습니다. Parametric Rectifier(PReLU)는 hyperparameter를 학습가능한 parameter로 바꾼 Activation Function입니다.
ELU (Exponential Linear Unit)

ReLU, Leaky ReLU는 원점에서 미분이 불가능하다는 문제가 있습니다. 정확히 원점인 상황은 거의 없기에 이를 무시하고 사용 가능하지만, 그래도 원점에서 미분 가능하도록 바꾼 것이 ELU입니다. ReLU의 모든 장점을 지니지만, 지수함수로 인해 계산이 복잡해지고 연산이 느려집니다.
Compare

위 그림은 Activation function별 CIFAR 10 데이터셋에 관한 정확도입니다. 미세한 정확도 차이가 존재하지만, 이는 데이터셋, 모델 구조 등에 따라 다르기에 절대적으로 우세한 Activation Function은 없습니다. Activation Function을 선택할 때 너무 깊게 생각하지 마시고 ReLU로 사용하시면 됩니다. 다만 Sigmoid / Tanh 함수는 사용하지 마세요!
Data Preprocessing

Input x가 2차원 점에 대응하면 위의 그림처럼 표현할 수 있습니다.
original data → zero-centered data(shifted) → normalized data(scaled)
zero-centered data는 original data에서 original data의 평균만큼을 이동하여 zero-centered 하게 만든 data입니다. normalized data는 zero-centered data를 표준편차로 나누어 정규화시킨 것입니다.

실제로는 PCA, Whitening을 통해 수행합니다.
*PCA는 대표적인 변수 추출 기법으로 상관관계가 없는 독립적인 축들로 구성됩니다. 따라서 decorrelated data를 만드는 과정이라고 볼 수 있습니다.

Data preprocessing을 하는 이유는 less sensitive, easy to optimize를 위해서 수행합니다. 정규화를 진행하지 않은 좌측의 그림에서는 미세한 기울기 변화가 큰 loss 변화를 만듭니다. 반면, 정규화를 진행한 우측은 less sensitive 합니다.
*파이썬 코드를 찾아보면 항상 training data만 정규화하고, testing data는 정규화하지 않았는데 오늘에야 알게 되었습니다.
Weight Initialization
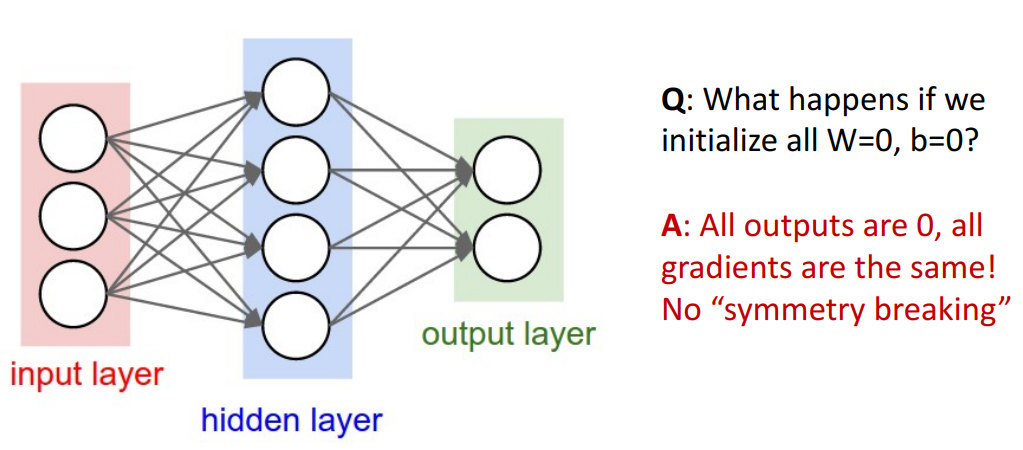
Data
Q. 만약 W=0, b=0에서 학습을 시작한다면 어떻게 될까요?
A. 모든 output은 0이 되고 모든 gradient는 똑같아질 것입니다.
따라서 각 노드들의 W, b가 조금씩 다르게 시작해야 합니다.

W를 평균=0, 표준편차=0.01인 정규분포를 따르는 random number로 설정하면 어떨까요?
작은 network에서는 잘 작동하지만, network가 deep 해질수록 잘 작동하지 않습니다.

처음 Layer에서는 표준편차가 상대적으로 큰 분포를 보이지만 Layer가 deep 해질수록 표준편차가 작아집니다. 평균=0이고 표준편차도 0에 근접해진다는 말은 Radom number도 0에 근접해질 확률이 높아짐을 의미합니다. 즉 update가 거의 이루어지지 않겠지요.

Xavier Initialization은 std를 1/sqrt(Din)로 설정하는 방법입니다. 꽤나 괜찮은 분포를 보이지 않나요?

하지만 우리가 주로 사용하는 ReLU에서 문제를 보입니다. ReLU는 x < 0인 분포를 모두 없애버리기 때문입니다.
Kaiming / MSRA Initialization은 Xavier Initialization에서 std 값에 변화를 주었습니다. 이로 ReLU를 보정해 주었습니다.
1/sqrt(Din) → sqrt(2 / Din)

ResNet에서 Weight Initialization을 진행하는 모습입니다.
Regularization
Dropout
Regularization은 overfitting을 해결하기 위해 사용하며, 앞서 L1, L2, Elastic net 등 여러 방법을 배웠습니다. 이번에는 Dropout을 배워보겠습니다.

Dropout은 forward pass에서 랜덤으로 몇몇의 뉴런을 0으로 만드는 것입니다. (연결을 하지 않음을 통해 학습에 반영하지 않는 것이겠죠?) 일반적으로 0.5의 확률로 결정합니다.

고양이를 분류하는 문제를 가정해 보겠습니다. 각 뉴런은 고양이의 특징을 보여주는데요, 이때 고양이의 모든 특징을 가지고 학습한다면 robust 하지 않습니다. 고양이의 특성이 바뀐다면 예측을 잘하지 못할 테니까요. 반면 dropout을 진행하면 여러 조합별 학습이 이루어져 robust 해집니다.


Test에서는 random으로 사용할 수는 없겠죠? 따라서 평균을 활용하고, 이를 종합해 보면 최종적으로는 1/2의 확률입니다.

8강에서 AlexNet과 VGG의 Fully-connected에서 파라미터가 가장 많음을 살펴보았습니다. 이때 Dropout을 수행하면 파라미터 수를 줄이는 효과를 볼 수 있을 것입니다. 다만 이후에 등장한 GoogLeNet부터는 flattening 대신 global average pooling이 사용되어 파라미터 수가 줄어들었기에 dropout을 사용하지 않습니다. 또한 2015년에 등장한 Batch Normalization이 Randomness를 추가하는 역할을 대신하기에 dropout을 사용하지 않는 경향이 늘어났습니다.
*dropout은 overfitting이 발생하기 쉬운 size가 큰 layer에서 사용합니다.
Data Augmentation
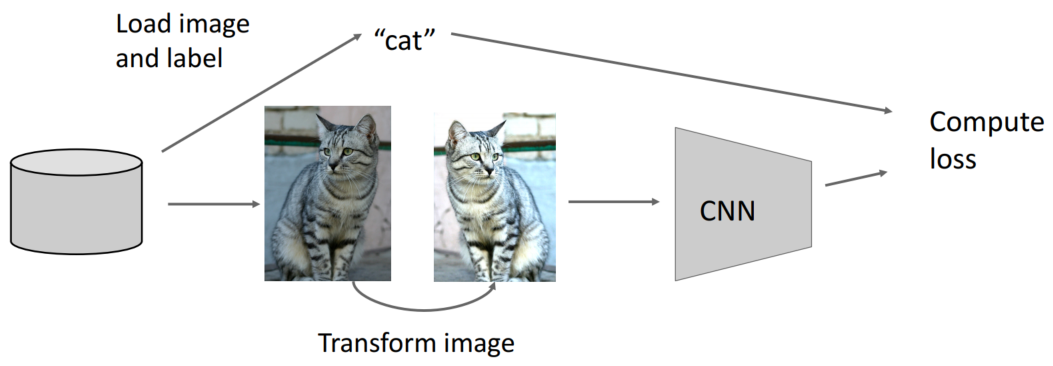
Data Augmentation도 Regularization의 일종으로 볼 수 있습니다. 특정 이미지를 대칭, 회전, 크기 변경 등을 통해 다른 이미지를 만들어내니 Randomness가 추가되는 것으로 생각할 수 있습니다. 이때 데이터에 맞게 적절한 기법을 사용해야 합니다. 예를 들어 왼손, 오른손을 분류하는 문제에는 horizontal flip을 사용할 수 없지만 고양이, 개를 분류하는 문제에는 horizontal flip을 사용할 수 있습니다.
mixup f베타 분포를 따르기에 0.6 -> 0.95 고양이 등이 가능함.