- 본 게시글은 Gilbert strang 교수님의 Linear Algebra, MIT 정리글입니다.
- 개인적인 공부를 위해 작성한 글이며, 잘못된 내용이 존재할 가능성이 있습니다.
- 잘못된 내용, 오타는 지적해 주시면 감사하겠습니다.
강의링크:
https://www.youtube.com/watch?v=JibVXBElKL0
이번 강의에서 살펴볼 내용은 다음과 같다.
- PA=LU
- vector spaces
- subspaces
이번 시간부터 vector를 넘어, vector 'space'를 살펴본다. 주의 깊게 들어야 할 부분이다.
PA=LU
이전 강의에서, no row exchanges 상황에서의 A = LU를 배웠다.
그러나 Permutation matrix, P를 사용하면 row exchanges가 가능해진다.
PA = LU
즉 '대부분'의 invertible A가 LU 분해 가능한 것을 넘어,
row exchanges를 통해 '모든' invertible A를 LU 분해가능하다는 의미인 것 같다.
참고로 permutation matrix의 의미를 다시 떠올려보자.
P= identity matrix with reordered rows,
그리고 n x n matrix에서 가능한 reorder은 n! 만큼 가능하다.
추가로, P는 다음과 같은 성질이 있다.
다음으로 Transpose이다.
Transpose의 정의는 다음과 같다.
row i는 column i로, column j는 row j로 바뀐다.
다음으로 Symmetric이다.
Symmetric matrix의 정의는 다음과 같다.
다음과 같은 matrix를 예로 들 수 있다.
그럼 Symmetric matrix는 언제 만들어질까?
의외로 신기하고 간단하며, 되돌아보면 자명하다.
모든 matrix R에 대해서 다음이 성립한다.
다음과 같은 예시를 보면 이해가 쉽다.
그럼 왜 R과 Transpose of R은 항상 Symmetric 할까?
그 이유는 바로 Transpose의 성질에 있다.
Transpose는 다음의 성질을 가지고 있다.
그리고 잠시 Symmetric matrix의 정의를 떠올려보면, !
똑같은 구조를 확인할 수 있다.
vector spaces & subspaces
: all column vector with n real components
R^2 예시를 통해 자세히 살펴본다.
: all 2-dim real vectors
R^2에는 다음과 같은 vector가 포함되어 있다.
하지만 만약
R^2에서 원점 (0,0)을 포함하지 않아도 vector space일까? 아니다.
그 이유는 vector space가 되기 위해서는
어떤 vector에 스칼라 곱을 하거나 선형 결합을 하여도
여전히 vector space에 존재하여야 하기 때문이다.
하지만 만약 원점(0,0)을 포함하지 않는다면 다음과 같은 상황에서 문제가 생긴다.
그리고 원점(0,0)은 원점을 포함하지 않는 R^2에는 존재 불가능하다.
따라서 만약 원점(0,0)을 포함하지 않는 R^2가 있다면, vector space가 아니다.
마찬가지로 xy평면에서 1 사분면만 고려하는 경우도 vector space가 아니다.
만약 음의 정수를 곱한다면 3 사분면에 속할 것이기 때문이다.
하지만 1 사분면을 subspace라고는 말할 수 있을까?
가능하다.
subspace of R^2는 a vector space inside R^2를 의미하기 때문이다.
Line in R^2 through zero vector도 마찬가지로 subspace of R^2이다.
하지만 여기서 중요한 점은 무조건 zero vector을 지나는 경우에만 해당된다는 점이다.
왜 그럴까?
zero vector을 지나지 않는 Line에 0을 곱해보자. 그럼 zero vector가 될 것이다.
그리고 zero vector은 zero vector을 지나지 않는 Line 위에 존재하지 않는다.
즉 정의를 충족하지 못하는 것이다.
따라서 모든 subspace도 zero를 포함해야만 한다.
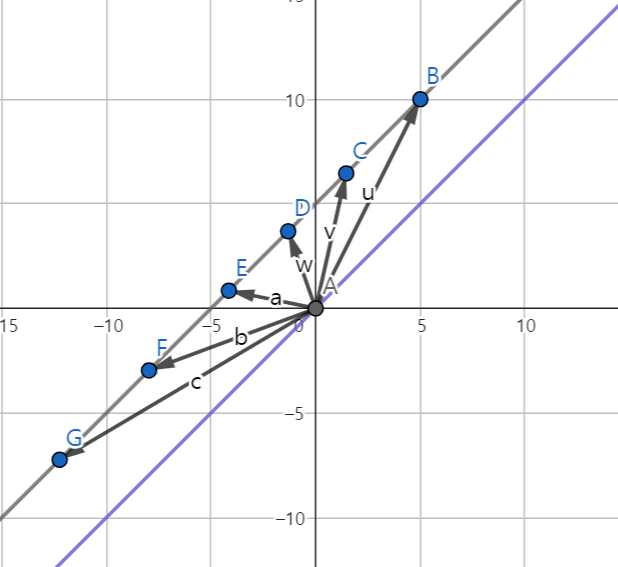
Subspaces of R^2에는 무엇이 있는지 생각해 보자.
1. all of R^2
2. any line through zero vector
(참고로 이때 line은 R^1의 line과는 다름. component를 2개 지니고 있기 때문)
3. zero vector only
zero vector only도 정의에 대입해 보면 자명하다.
zero vector에 1,3,5 등을 곱하여도 여전히 zero vector이고,
zero vector+ zero vector도 zero vector이기 때문이다.
그럼 Subspaces of R^3에는 무엇이 있을까? 차원이 확장되었기에, 다음과 같이 될 것이다.
1. all of R^3
2. any plane through zero vector
3. any line through zero vector
4. zero vector only
다음과 같은 matrix가 있다고 하자. 이를 column picture로 보면 col 1, col 2로 볼 수 있다.
그리고 columns들은 R^3에 있다.
이때
all therir combinations from a subspace를 column space, C(A)
라고 부른다.

같이 읽으면 좋은 자료
벡터 공간 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 다른 뜻에 대해서는 벡터 문서를 참고하십시오. 선형대수학에서 벡터 공간(vector空間, 영어: vector space, 문화어: 벡토르공간, 선형공간[1][2]) 또는 선형 공간(線型
ko.wikipedia.org
[Linear Algebra] Lecture 6 Column Space와 영공간(Null Space)
이번 포스팅에서는 Column Space와 Null Space에 대해 설명할 것이다. 컬럼 공간, 영공간으로 각각 한글화 시킬 순 있지만 뭔가 어색하기 때문에 그냥 컬럼 스페이스, 널 스페이스로 읽도록 하겠다. Colu
twlab.tistory.com
'공부 정리 > Linear Algebra' 카테고리의 다른 글
| [MIT Linear Algebra] 7. Solving Ax = 0: Pivot Variables, Special Solutions (1) | 2024.01.15 |
|---|---|
| [MIT Linear Algebra] 6. Column Space and Nullspace (1) | 2024.01.13 |
| [MIT Linear Algebra] 4. Factorization into A = LU (0) | 2024.01.11 |
| [MIT Linear Algebra] 3. Multiplication and Inverse Matrices (1) | 2024.01.10 |
| [MIT Linear Algebra] 2. Elimination with Matrices (1) | 2024.01.08 |